Достаточно проверить выполнение равенства

.
Положим Ах₁=у₁ и Ах₂=у₂, в силу линейности А имеем
(*)
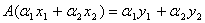По определению обратного оператора А^-1у₁=х₁ и А^-1у₂=х₂, умножим оба равенства соответственно на и :
.
С другой стороны из равенства (*) следует , следовательно, .
Теорема доказана.
Теорема 4 [3]. (Теорема Банаха об обратном операторе)
Пусть А – линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство Е на банахово пространство Е₁. Тогда обратный оператор А^-1 ограничен.
Теорема 5 [3]. Пусть Е – банахово пространство, I – тождественный оператор в Е, а А – такой ограниченный линейный оператор, отображающий Е в себя, что 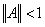. Тогда оператор (I-A) ^-1 существует, ограничен и представляется в виде .
Доказательство.
Так как 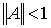, то ряд сходится. А так как для всех 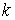, то ряд также сходится. Пространство Е полно, значит, из сходимости ряда вытекает, что сумма ряда представляет собой ограниченный линейный оператор. Для любого n имеем: , переходя к пределу и учитывая, что , получаем , следовательно .
Теорема доказана.

67 Матричная запись линейных операторов.

Выберем в пространстве V базис . Пусть – произвольный элемент из V и – разложение по данному базису. Пусть А – линейный оператор из . Тогда А А . Полагая, что

А (7.1)

получим

А

Таким образом, если А и элемент имеет координаты , то

(7.2)

Рассмотрим квадратную матрицу А с элементами : Эта матрица называется матрицей линейного оператора в заданном базисе .

Наряду с ранее указанным способом записи линейного оператора А используется, при заданном базисе , следующая матричная форма: , причем, если , то , где , , определяется с помощью соотношения (7.2), а элементы матрицы А определяются по формулам (7.1).

1. Прямоугольные (декартовы) координаты на прямой, плоскости и в пространстве. Косоугольные системы координат.

2. Расстояние между двумя точками прямой, плоскости и в пространстве.

3. Деление отрезка в заданном отношении.

4. Полярная система координат. Сферическая система координат.

5. Переход от декартовой к полярной системе координат и обратно.

6. Преобразование координат для прямоугольной системы координат.

7. Алгебраическая линия и её порядок. Теорема об инвариантности порядка.

8. Уравнение прямой на плоскости, проходящей через две заданные точки.

9. Уравнение прямой с угловым коэффициентом. Пучок прямых.

10. Уравнение прямой, проходящей через заданную точку в заданном направлении.

11. Угол между двумя прямыми.

12. Условия параллельности и перпендикулярности прямых.

13. Уравнение прямой в отрезках на осях.

14. Общее уравнение прямой на плоскости.

15. Окружность. Общее и каноническое уравнения окружности.

16. Эллипс. Каноническое уравнение эллипса и его свойства.

17. Парабола. Каноническое уравнение параболы и его свойства.

18. Гипербола. Каноническое уравнение гиперболы и его свойства.

19. Окружность, эллипс, гипербола и парабола как алгебраические линии второго порядка.

20. Геометрический вектор (длина вектора, нуль-вектор, равенство геометрических векторов, коллинеарность и компланарность). Координатные орты.

21. Линейные операции с геометрическими векторами. Координаты геометрического вектора. Радиуса-вектор.

22. Разложение произвольного вектора по ортам координат­ных осей на плоскости и в пространстве.

23. Действия с геометрическими векторами в координатной форме.

24. Признак коллинеарности векторов.

25. Скалярное произведение геометрических векторов и его свойства.

26. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.

27. Общее уравнение прямой на плоскости в представлении геометрических векторов.

28. Каноническое и параметрическое уравнения прямой в пространстве.

29. Общее уравнение плоскости в пространстве.

30. Решение неравенств на плоскости.

31. Матрицы и их классификация. Действия с матрицами. Экономические примеры.

32. Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».

33. Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.

34. Свойства определителя. Терема об определителе произведения квадратных матриц.

35. Обратная матрица. Теорема существования и единственности обратной матрицы.

36. Элементарное преобразование матрицы. Элементарное преобразования матрицы как умножение матриц.

37. Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.

38. Транспонирование и его свойства.

39. Система линейных уравнений и её решение.

40. Теорема об элементарных преобразованиях системы линейных уравнений. Метод Гаусса для решений совместной системы линейных уравнений.

41. Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.

42. Теорема о решении однородной системы линейных уравнений.

43. Теорема о числе решений совместной системы линейных уравнений.

44. Решение квадратной системы линейных уравнений с помощью обратной матрицы.

45. Формулы Крамера.

46. Линейное (векторное) пространство. Линейное подпространство.

47. Пространство Rⁿ и линейные операции в этом пространстве.

48. Система векторов. Линейно зависимые и независимые векторы.

49. Базис линейного пространства. Примеры.

50. Теорема о разложении вектора по базису.

51. Линейная оболочка векторов.

52. Векторное представление системы линейных уравнений.

53. Теорема Кронекера-Капелли.

54. Критерий линейной зависимости векторов в пространстве Rⁿ.

55. Евклидовое пространство.

56. Нормируемое пространство.

57. Ортогональное дополнение и его свойства.

58. Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.

59. Линейная функция. Билинейная форма. Квадратичная форма.

60. Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.

61. Линейная балансовая модель.

62. Модель международной торговли.

63. Комплексные числа. Формула Эйлера. Решение комплексных неравенств на плоскости.

64. Линейные операторы как отображения. Образ и ядро линейного оператора.

65. Взаимно однозначные отображения.

66. Произведение операторов. Обратный оператор.

67. Матричная запись линейных операторов.

Поиск по сайту: