 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема о числе решений совместной системы линейных уравнений
?
Решение квадратной системы линейных уравнений с помощью обратной матрицы.
Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X1 - n не будет равен нулю. Посчитаем этот определитель. Если он равен нулю, то система не будет иметь однозначного, единственного решения и программа не будет решать дальше и выдаст сообщение об ошибке. Если определитель не равен нулю, то будем решать дальше методом обратной матрицы.
Записанную Вами систему можно представить в виде произведения матриц:
A × X = B, где X - матрица, содержащая искомые Вами решения системы уравнений.
Найдем матрицу, обратную матрице A, как известно - А-1 × A = E, где Е - единичная матрица (квадратная матрица с единицами на главной диагонали), эквивалент '1' в матричном исчислении.
Домножим обе части уравнения слева на А-1.
А-1 × A × X = А-1 × B.
Е × X = А-1 × B.
X = А-1 × B.
Пример
| - x 1 | + 2x 2 | = 6 | |
| - x 1 | + 3x 2 | + 7x 3 | = 9 |
| - x 1 | + x 2 | + x 3 | = 3 |
Решение
Найдем определитель главной матрицы, составленной из коэффициентов при X1 - n:
| = -8 |
Определитель главной матрицы системы уравнений не равен нулю, следовательно данная система уравнений имеет единственное решение. Найдем его.
Согласно описанному выше методу необходимо найти матрицу, обратную матрице, составленной из коэффициентов при элементах X1 - n. Для этого достроим главный определитель единичной квадратной матрицей того же порядка справа и последовательно, при помощи элементарных преобразований перенесем единичную квадратную матрицу справа налево. Квадратная матрица, получившаяся при этом справа и будет обратной к главной. Затем домножим обратную матрицу на матрицу В (значения находящие за знаком равенства) и получим матрицу решений.
Достраиваем единичную матрицу справа.
|
Найдем обратную матрицу.
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
|
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1. Квадратная матрица, получившаяся правее единичной и есть обратная к главной.
|
Умножение обратной матрицы (матрицы - А-1) на матрицу значений за знаком равенства (матрицу - В).
| × | = |
Ответ
| x 1 = 0 |
| x 2 = 3 |
| x 3 = 0 |
45 Формулы Крамера.
xi=Δi\Δ. Δ1 получена из Δ путем замены первого столбца коэффициентов столбцом из свободных членов.
Записываем матричное равенство в виде: (х1)=1\Δ (А11 А12 А13) × (b1). записана первая строка,нижние по аналогии. Далее внесем определитель и свободные члены в основную матрицу. Отсюда следует: х1=А11b1+A12b2+… (нижние строки по аналогии). Но А11b1+A12b2+… есть разложение определителя по элементам первого столбца. Значит см.выше.
46Линейное (векторное) пространство. Линейное подпространство.
Векторное (линейное) пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трехмерного пространства.
Векторным пространством (над полем R или C) называют множество L, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные (комплексные) числа, удовлетворяющие следующим условиям:
1) x + y = y + x (коммутативность сложения);
2) (x + y) + z = x + (y + z) (ассоциативность сложения);
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x для любого вектора x;
4) для любого вектора x существует противоположный ему вектор y такой, что x + y = 0;
5) 1∙x = x;
6) α(βx) = (αβ)x (ассоциативность умножения);
7) (α + β)x = αx + βx (дистрибутивность относительно числового множителя);
8) α(x + y) = αx + αy (дистрибутивность относительно векторного множителя).
47Пространство Rn и линейные операции в этом пространстве.
Векторное пространство называют. n-мерным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e1, e2,...en, а любые n+1 элементов линейно зависимы. Векторное пространство называют бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мерного векторного пространства образуют базис этого пространства. Если e1, e2,...en - базис векторного пространства, то любой вектор x этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:
x = α1e1 + α2e2 +... + αnen.
При этом числа α1, α2,...,αn называют координатами вектора x в данном базисе.
Множество всех векторов 3-мерного пространства образует векторное пространство. Более сложным примером может служить так называемое n-мерное векторное пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел (λ1, λ2,..., λn). Сумма двух векторов и произведение на число определяются соотношениями:
(λ1, λ2,..., λn) + (μ1, μ2,..., μn) =
= (λ1 + μ1, λ2 + μ2,..., λn + μn),
α∙(λ1, λ2,..., λn) = (α∙λ1, α∙λ2,..., α∙λn).
Базисом в этом пространстве может служить, например, следующая система из n векторов: e1 = (1, 0,..., 0), e2 = (0, 1,..., 0),...en = (0, 0,..., 1).
48 Система векторов. Линейно зависимые и независимые векторы.
Пусть имеем векторное пространство V и систему векторов A={  } (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор
} (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор  называется линейной комбинацией системы векторов A. Если все скаляры α1 = α2 = α3... = αk = 0, то такая комбинация называется тривиальной (простейшей), (и
называется линейной комбинацией системы векторов A. Если все скаляры α1 = α2 = α3... = αk = 0, то такая комбинация называется тривиальной (простейшей), (и  ). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной
). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной
Определение 1. Система векторов A называется линейно-независимой, если только тривиальная линейная комбинация векторов системы равна  (т.е.
(т.е.  )
)
Определение 2. система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная 
Критерий линейной зависимости векторов:
Для того чтобы векторы  (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
Размерность линейного пространства
Линейное пространство V называется n-мерным (имеет размерность n), если в нем:
1) существует n линейно независимых векторов;
2) любая система n + 1 векторов линейно зависима.
49 Базис линейного пространства. Примеры.
Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
1) система линейно независима.
2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов)
Базис в пространстве R в степени n (канонический базис). Примеры: Базисом в пространстве называются три некомпланарных вектора, взятые в определённом порядке. Эти векторы называются базисными.
50 Теорема о разложении вектора по базису.
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Определение. Пусть а – произвольный вектор,  - произвольная система векторов. Если выполняется равенство
- произвольная система векторов. Если выполняется равенство
 (1)
(1)
то говорят, что вектор а представлен в виде линейной комбинации данной системы векторов. Если данная система векторов  является базисом векторного пространства, то равенство (1) называется разложением вектора а по базису
является базисом векторного пространства, то равенство (1) называется разложением вектора а по базису  .
.
Коэффициенты линейной комбинации  называются в этом случае координатами вектора а относительно базиса
называются в этом случае координатами вектора а относительно базиса 
51 Линейная оболочка векторов.
Пусть  - система векторов из векторного пространства V над полем P.
- система векторов из векторного пространства V над полем P.
Определение 2: Линейной оболочкой L системы A называется множество всех линейных комбинаций векторов системы A. Обозначение L(A).
Можно показать, что для любых двух систем A и B,
1. A линейно выражается через B тогда и только тогда, когда 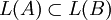 . (1)
. (1)
2. A эквивалентна B тогда и только тогда, когда L(A)=L(B). (2)
Доказательство следует из предыдущего свойства
3 Линейная оболочка любой системы векторов является подпространством пространства V.
Доказательство
Возьмём любые два вектора  и
и  из L(A), имеющие следующие разложения по векторам из A:
из L(A), имеющие следующие разложения по векторам из A:  . Проверим выполнимость условий 1) и 2) критерия:
. Проверим выполнимость условий 1) и 2) критерия:
1.  , так как представляет собой линейную комбинацию векторов системы A.
, так как представляет собой линейную комбинацию векторов системы A.
2.  , так как тоже представляет собой линейную комбинацию векторов системы A.
, так как тоже представляет собой линейную комбинацию векторов системы A.
Рассмотрим теперь матрицу  . Линейная оболочка строк матрицы A называется строчечным пространством матрицы и обозначается Lr(A). Линейная оболочка столбцов матрицы A называется столбцовым пространством и обозначается Lc(A). Обратите внимание, что при
. Линейная оболочка строк матрицы A называется строчечным пространством матрицы и обозначается Lr(A). Линейная оболочка столбцов матрицы A называется столбцовым пространством и обозначается Lc(A). Обратите внимание, что при  строчечное и столбцовое пространство матрицы A являются подпространствами разных арифметических пространств Pn и Pm соответственно. Пользуясь утверждением (2), можно придти к следующему выводу:
строчечное и столбцовое пространство матрицы A являются подпространствами разных арифметических пространств Pn и Pm соответственно. Пользуясь утверждением (2), можно придти к следующему выводу:
Теорема 3: Если одна матрица получена из другой цепочкой элементарных преобразований, то строчечные пространства таких матриц совпадают.
52 Векторное представление системы линейных уравнений.
53 Теорема Кронекера-Капелли.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений
Правило решения произвольной системы уравнений. Найти ранг основной и расширенной матриц,если они не равны,то система несовместна(нет решений). Найти какой-либо базисный минор порядка r. Взять r уравнений из коэффициентов которых составлен базисный минор(остальные отбросить). Коэффициенты которые входят в базисный минор-главные,записываются слева, остальные переносятся в правые части уравнений(свободные). Далее найти выражения главных неизвестных через свободные. Получается общее решение системы. Затем придавая свободным неизвестным произвольные значения получим соответствующие значения главных неизвестных(частные решения исходной системы).
54 Критерий линейной зависимости векторов в пространстве Rn.
Линейная комбинация векторов
Линейной комбинацией векторов 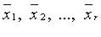 называют вектор
называют вектор

где  - коэффициенты линейной комбинации. Если
- коэффициенты линейной комбинации. Если  комбинация называется тривиальной, если
комбинация называется тривиальной, если  - нетривиальной.
- нетривиальной.
Поиск по сайту: