Система линейных уравнений и её решение

Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида:

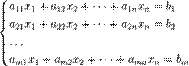
Где числа 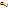, , называется коэффициентами системы числа – свободными членами. Подлежат нахождению числа .

Такую систему удобно записывать в компактной матричной форме А*Х=В.

Здесь А – матрица коэффициентов системы, называемая основной матрицей:

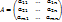
–вектор-столбец из неизвестных ,

– вектор-столбец из свободных членов .

Произведение матриц А*Х определено, т.к. в матрице А столбов столько же, сколько строк в матрице Х.

Решением системы называется n значений неизвестных , ,…….., , при подстановке которых все уравнения системы обращаются в верные неравенства. Всякое решение системы можно записать в виде матрицы-столбца

.

Поиск по сайту: