АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений

Читайте также:
  1. I. Суспільство як соціальна система.
  2. I. Формирование системы военной психологии в России.
  3. II. Цель и задачи государственной политики в области развития инновационной системы
  4. II. Экономические институты и системы
  5. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  6. SCADA-системы
  7. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  8. TRACE MODE 6: компоненты инструментальной системы
  9. А). Системы разомкнутые, замкнутые и комбинированные.
  10. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  11. Абиотические компоненты экосистемы.
  12. Абстрактные линейные системы

Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.

Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x1=0, x2=0,..., xn=0.

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет не одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет больше одного решения.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Система линейных уравнений может быть представлена в матричной форме как:

или:

.

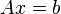Здесь 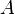— это матрица системы, — столбец неизвестных, а — столбец свободных членов. Если к матрице 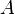приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)