Абстрактные линейные системы

Хотя многие понятия теории систем и можно определить, опираясь исключительно па понятие общей системы, получение содержательных математических результатов становится возможным только после введения дополнительных структур. Чтобы избежать чрезмерного количества определений, мы будем, как правило, вводить конкретные понятия па том же уровне общности, на котором для них можно получить нетривиальные математические результаты. Например, понятие динамической системы будет введено лишь в контексте временных систем. Тем не менее понятие линейности оказывается полезным уже на любом уровне общности. Поэтому мы определим это понятие сейчас и будем пользоваться им как стандартным.

Пусть — А некоторое поле, X и Y – линейные алгебры над A, S – отношение, 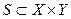, причем S непусто. Пусть, кроме того,

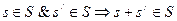
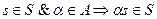
где + обозначает (внутреннюю) операцию сложения в X х Y,а через as обозначен результат (внешней) операции умножения на скаляр. Тогда S называется (абстрактной) полной линейной системой.

Пусть X и Y – линейные алгебры над одним и тем же полем А. Система 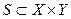является линейной в том и только в том случае, когда найдется такая глобальная реакция 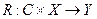, что

1) С есть линейная алгебра над А.

2)Существует пара таких линейных отображени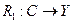й и 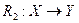, что для всех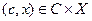

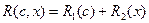
Пусть 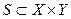- линейная система, a R – отображение, 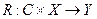. Отображение называется линейной глобальной реакцией системы тогда и только тогда, когда

1) R согласуется с S, т. е.

2) С является линейной алгеброй над полем А скаляров линейных алгебр X и Y.

3) существуют два таких линейных отображения 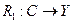и 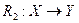, что для любых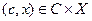

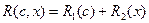
В этом случае С называют линейным объектом глобальных состояний, отображение 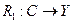– глобальной реакцией на состояние, a 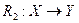– глобальной реакцией на вход.

Общие временные и динамические системы

Общие временные системы

Чтобы ввести понятие общей временной системы, нужно формализовать понятие времени. В соответствии с нашей общей стратегией мы должны определить понятие времени, используя «минимальную» математическую структуру, отражающую при этом

наиболее существенные черты наших интуитивных представлений о времени. Эта задача кажется очень простой, однако то, как мы решим ее, самым решающим образом сказывается на всем последующем. Выбор структуры для такого фундаментального понятия, как множество моментов времени, оказывает существенное влияние на дальнейшее развитие теории, а также на богатство и изящность получаемых математических результатов. Здесь мы определим это понятие следующим образом.

Множеством моментов времени (общей временной системы) называется линейно упорядоченное (абстрактное) множество. Это множество будет обозначаться символом Т, а определенное в нем отношение порядка — через ≤.

Легко видеть, что минимальным свойством, присущим множеству моментов времени, мы считаем здесь то, что его элементы следуют один за другим в вполне определенном порядке. Это отражает наше стремление использовать понятие времени для изучения эволюции поведения системы. Отметим, что на мощность множества моментов времени мы не налагаем никаких ограничений. Однако может оказаться необходимым задавать на множестве моментов времени какие-то дополнительные структуры, например структуру абелевой группы. Такие дополнительные предположения мы будем вводить по мере их необходимости.

Для удобства обозначений мы будем считать, что в множестве Т имеется минимальный элемент 0. Другими словами, мы предполагаем, что существует некоторое надмножество , линейно упорядоченное отношением ≤ и содержащее фиксированный элемент 0, такой, что множество Т можно определить как Т={t: t ≥0}

Введем теперь еще одно определение.

Пусть А и В - - какие-то произвольные множества, Т некоторое множество моментов времени, А^T и В^T – множества всевозможных отображений из Т в А и В соответственно и 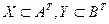. Общей временной системой S над X и Y называется отношение на X и Y, т. е. 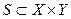. Множества А и В называются алфавитами входных воздействий (входов) и выходных величин (выходов) системы соответственно. Множества X и Y называют еще временными объектами системы; их элементами и служат абстрактные функции времени. Значения функций из X и Y в момент времени t будут соответственно обозначаться через х(t)и y(t).

Для того чтобы изучать динамику поведения временных систем, необходимо ввести в рассмотрение подходящие для этой цели отрезки (интервалы) времени. В этой связи мы договоримся пользоваться следующими обозначениями.

Для любых t, t' > t

, , , ,

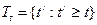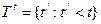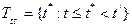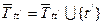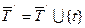
Сужение функций на различные отрезки времени будут определяться следующим образом:

, , , ,

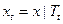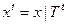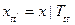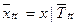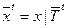
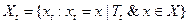
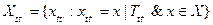
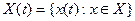
Так же договоримся, что

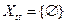
С помощью операции сужения мы введем новую операцию – операцию сочленения. Пусть 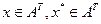. Тогда для любого t можно определить новый элемент из А^т, положив

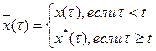
и условившись обозначать через = х' • . Последнюю операцию и называют операцией сочленения элементов х' и ,

Для заданного множества семейство всевозможных определенных выше сужений элементов из X мы будем обозначать через X. Другими словами,

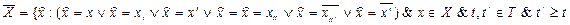
Сужения функций из Y и соответствующие операции в Y определяются точно так же, как и в X.

Временная система 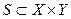называется системой с полным входом тогда и только тогда, когда

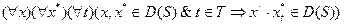и

В последующем мы всегда будем предполагать, что все рассматриваемые общие временные системы относятся к категории систем с полным входом, если только явно не оговорено противное.

Сужения временной системы S определяются через сужения ее входных воздействий и выходных величин:

,

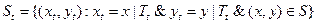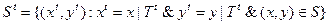
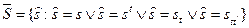
Мы будем пользоваться еще и следующими условными обозначениями:

, ,

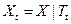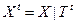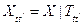
Аналогичные обозначения вводятся для Y и S. Например,

, ,

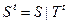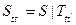
Пусть S — временная система, 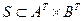. Объектом начальных состояний системы S и начальной реакцией системы называются соответственно объект глобальных состояний и глобальная реакция этой системы. Начальная реакция системы обозначается через р₀. Другими словами, удовлетворяет условию

Пусть S - - временная система и 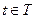. Объектом состояний в момент времени t, который мы будем обозначать через С_t называется объект начальных состояний для сужения S_t. Другими словами, это абстрактное множество, для которого найдется такая функция 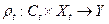, что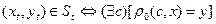

Функцию р_t, называют реакцией (системы) в момент времени t. Семейство всех реакций данной системы, т. е.

назовем семейством реакций системы S, а множество 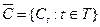семейством объектов состояний.

Пусть S – временная система, и 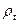– некоторая функция, такая, что 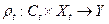Мы будем говорить, что р, согласуется с S тогда и только тогда, когда она совпадает с реакцией системы S в момент времени t, т. е. когда

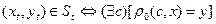
Пусть

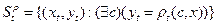
Тогда условие согласованности можно переписать в виде

Пусть 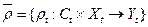- семейство произвольных функций. Мы будем говорить, что согласуется с временной системой S тогда и только тогда, когда совпадает с семейством реакций системы S, т. е. когда для любого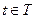

Пусть - семейство произвольных отображений. Для существования временной системы , согласующейся с (т. е. должно быть семейством реакций системы S), необходимо и достаточно, чтобы для всех 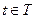выполнялись следующие условия:

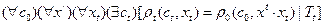
Общие динамические системы

Понятие динамической системы возникает тогда, когда появляется необходимость исследовать, как система развивается во времени. Поэтому нужно установить взаимосвязь между значениями объектов системы, относящимися к различным моментам времени. Для этой цели одного понятия реакции системы уже недостаточно и приходится вводить другое семейство функций.

Временная система называется динамической (или она допускает динамическое представление) тогда и только тогда, когда найдутся два таких семейства отображений

И

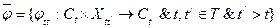
Что

1) семейство согласуется с S, т. е. является семейством реакций этой системы.

2) все функции , из семейства удовлетворяют следующим условиям:

;

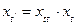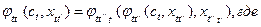
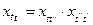
Поиск по сайту: