Для линейной модели

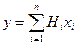
для дестабилизирующего фактора α_s, воздействующего на Н_i и x_i, имеем

.

В результате эквивалентных преобразований с учетом x_i=y/H_i получаем

.

Таким образом,

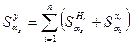
или относительное отклонение по аналогии равно

.

В случае, если угрозы Т воздействуют только на ресурсы системы х_i, получаем

.

Наоборот при воздействии на инфраструктуру Н_i имеем

.

Если пороги безопасности заданы в относительном виде

,

получаем

.

Отсюда при прогнозируемом относительном отклонении дестабилизирующего фактора Δα_s/α_s = необходимым условием обеспечения безопасности системы является

.

Снижение значений коэффициента чувствительности будет способствовать увеличению запаса устойчивости системы. Это радикальная стратегия защиты. Однако дороговизна этого проекта вынуждает осуществлять данный подход селективно. Отсюда механизмы защиты М уместно активно применять к каналам, где коэффициенты чувствительности наиболее высоки. Именно они являются в данном случае объектами особой уязвимости при воздействии Т.

В случае, когда вместо α_s используется целый ансамбль факторов А, соответствующее выражение примет вид

.

Однако выводы по критериям безопасности не претерпят принципиальных изменений. Соответствующие выражения могут быть получены.

Поиск по сайту: