Лекция 4-5. Методы представления систем

Классификации методов формализованного представления систем. В большинстве первоначально применявшихся при исследовании систем классификаций выделяли детерминированные и вероятностные (статистические) методы или классы моделей, которые сформировались в конце прошлого столетия. Затем появились классификации, в которых в самостоятельные классы выделились теоретико-множественные представленыя, графы, математическая логика и некоторые новые разделы математики.

В одной из первых классификаций, предложенных специально для целей системных исследований наряду с выделением таких уровней математического абстрагирования, как общеалгебраический, теоретика-множественный, логико-лингвистический, предлагается рассматривать информационный и эвристический уровни изучения сложных систем.

Рассмотрим классификацию, в которой выделяются следующие обобщенные группы (классы) методов (табл. 1):

• аналитические, к которым в рассматриваемой классификации отнесены методы классической математики, включая интегро-дифференциальное исчисление, методы поиска экстремумов функций, вариационное исчисление и т. п; методы математического программирования; первые работы по теории игр и т. п.;
• статистические, включающие и теоретические разделы математики - теорию вероятностей, математическую статистику, и направления прикладной математики, использующие стохастические представления - теорию массового обслуживания, методы статистических испытаний,
• теоретико-множественные, логические, лингвистические, семиотические представления (методы дискретной математики), составляющие теоретическую основу разработки языков моделирования, автоматизации проектирования, информационно-поисковых языков;
• графические, включающие теорию графов и разного рода графические представления информации типа диаграмм, гистограмм и других графиков.

Разумеется, в табл. 1 приведены лишь укрупненные группы-направления, конкретные методы которых только в начальный период развития характеризуются рассмотренными особенностями. Эти направления непрерывно развиваются, и в их рамках появляются методы с расширенными возможностями по сравнению с исходными.

В частности, на пересечении аналитических и теоретико-множественных представлений возникла и развивается алгебра групп; параллельно в рамках алгебры групп и теории множеств начала развиваться комбитаторика; теоретико-множественные и графические представления стали основой возникновения топологиических, статистические и теоретико-множественные методы инициировали возникновение теории размытых множеств, которая, в свою очередь, явилась началом развития нового направления - нечетких формализаций и т.д.

Практически невозможно создать единую классификацию, которая включала бы все разделы современной математики. В то же время приведенные направления помогают понять особенности конкретных методов, использующие средства того или иного направления или их сочетания, помогают выбирать методы для конкретных приложений.

Название	Символический образ	Основная терминология и примеры теорий, возникших и развивающихся на базе соответствующего класса методов	Сферы и возможности применения
Аналитический		Аналитическими здесь названы методы, которые ряд свойств многомерной, многосвязной системы отображают в n-мерном пространстве в виде одной единственной точки (безразмерной в строгих математических доказательствах), совершающей какие-либо перемещения в пространстве (или обладающую каким-то поведением). Это отображение осуществляется посредством оператора (функции, функционала) Ф[Sx]. Можно также две (или более) системы или их части отобразить точками и рассматривать взаимодействие этих точек. Поведение точек, их взаимодействие описываются строгими соотношениями, имеющими силу закона. Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т. д.). На базе аналитических представлений возникли и развиваются математические теории различной сложности от аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т.п.) до таких новых разделов современной математики, как математическое программирование (линейное, нелинейное, динамическое ч т. п.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т, п.)	Применяются в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин или зависимостей, т. е. когда знания о процессах и событиях в некотором интервале времени позволяют полностью определить поведение их вне этого интервала. Эти методы используются при решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего пути, оптимальной стратегии поведения, в том числе в конфликтных ситуациях ит.п. Математические теории, развивающиеся на базе аналитических представлений, направления стали основой многих прикладных теорий, в том числе теории автоматического управления, теории оптимальных решений и т. д. При практическом применении аналогических представлений для отображения сложных систем следует иметь в виду, что они требуют установления всех детерминированных связей между учитываемыми компонентами и целями системы в виде аналитических зависимостей. Для сложных многокомпонентных, многокритериальных систем получить требуемые аналитические зависимости крайне трудно. Более того, даже если это и удается, то практически невозможно доказать правомерность применения таких выражений, т. е. адекватность модели рассматриваемой задаче
Статический		Статистическим называют отображение системы с помощью случайных (стохастических событий, процессов, которые описываются вероятностными характеристиками и статистическими закономерностями. Статистические отображения системы можно представить как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (ее учитываемые в модели свойства) оператор Ф[Sx], «Размытую» точку следует понимать как некоторую область, характеризующую движение системы (ее поведение); при этом границы области заданы с некоторой вероятностью р (под вероятностью события понимается р(А)=:т/п, где т - число появлений события A, n - общее число опытов), т. е, как бы размыты, и движение точки описывается некоторой случайной функцией Закрепляя все параметры этой области, кроме одного, можно получить срез по линии а- b смысл которого - воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру, Аналогично можно получить двумерную, трехмерную и т.д. картины статистического распределения.	На базе статистических представлений возникли и развиваются прикладные направления: статистическая радиотехника, статистическая теория распознавания образов, экономическая статистика, теория массового обслуживания а также развившиеся из направлений, возникших на базе аналитических представлений, стохастическое программирование новые разделы теории игр и т. п. Расширение возможностей отображения сложных систем и процессов по сравнению с аналитическими методами можно объяснить тем, что при применении статистических представлений процесс постановки задачи как бы частично заменяется статистическими исследованиями, позволяющими, не выявляя все детерминированные связи между изучаемыми объектами (событиями) или учитываемыми компонентами сложной системы, на основе выборочного исследования (исследования репрезентативной выборки получать статистические закономерности ираспространять ихна поведение системы вцелом с какой-товероятностью). Однако не всегда можно получить статистические закономерности, не всегда может быть определена репрезентативная выборка; доказана правомерность применения статистических закономерностей. Если же не удается доказать репрезентативность выборки или для этого требуется недопустимо большое время, то применение статистических методов может привести к неверным результатам. В таких случаях целесообразно обратиться к методам, объединяемым под общим названием методы дискретной математики, которые помогают разрабатывать языки моделирования, модели и методики постепенной формализации процесса принятия решения. Статистические и теоретико-множественные методы инициировали возникновение теории нечетких или размытых множеств Л. Заде, которая явилась началом развития нового направления - нечетких формализации
		На базе статистических представлений развивается ряд математических теорий: математическая статистика; теория статистических испытаний, а развитием - теория статистического имитационного моделирования, теория выдвижения и проверки статистических гипотез, базирующаяся на общей теории статистических решающих функций (частным случаем этой теории, важным для теории систем, является байесовский подход к исследованию передачи информации в процессах общения, обучения и др. ситуациях); теория потенциальной помехоустойчивости и теории решающих функций', обобщение последних двух направлений -теория статистических решений
Теоретико-множественные		Теоретико-множественное представления базируются на понятиях множество, элементы множества, отношения на множествах, континуум. Множества могут задаваться следующими способами: 1) перечислением (интенсионально): {a}, где j = 1...и или <a1, a2,..., ai,...,аn>, где аi€A 2) путем указания некоторого характеристического свойства А (экстенсионально). В основе теоретико-множественных преобразований лежит переход от одного способа задания множества к другому: В множестве могут быть выделены подмножества. Из двух или нескольких множеств можно сформировать путем установления отношений между элементами этих множеств новое множество, обладающее принципиально новыми свойствами и, как прави­ло, новое качество приобретают и элементы. Теоретико-множественные представления допускают введение любых произвольных отношений. При конкретизации отношений и правил их использования можно получить одну из алгебр логики, один из формальных языков математической лингвистики, создать язык моделирования сложной системы, который затем, получив соответствующее название может развиваться как самостоятельное научное направление. Между теоретико-множественными описаниями разных систем или их частей можно устанавливать соответствия: гомоморфизма, изоморфизма, автоморфизма отношения рефлексивности, симметричности, транзитивности, заимствованные теорией множеств из других разделов математики	Благодаря возможности введения любых отношений теоретико-множественные представления используются как обобшаюший язык при сопоставлении различных направлений математики и других дисциплин, явились основой для возникновения новых научных направлений или развития существующих, Система может быть представлена совокупностью множеств или подмножеств разнородных компонентов с произвольно вводи­мыми элементами и отношениями. Однако свобода введения произвольных отношений приводит к тому, что в формализованном с их помощью описании проблемной ситуации довольно быстро могут обнаружиться неразрешимые противоречия - парадоксы, апории или антиномии, что не позволяет оперировать с получаемыми теоретико-множественными моделями таким же образом, как с классическими математическими (аналитическими, статистическими) соотношениями, гарантируя достоверность получаемых результатов
Логический		Логические представления переводят реальную систему и отношения в ней на язык одной из алгебр логики (двузначной, многозначной), основанной на применении алгебраических методов для выражений законов алгебры логики. Наибольшее распространение получила бинарная алгебра логики Буля (булева алгебра). Базовыми понятиями алгебры логики являются: высказывание, предикат, логические функции (операции) кванторы, логический базис, логические законы или теоремы (законы алгебры логики), применяя которые можно преобразовать систему из одного описания в другие с целью ее совершенствования. Например, получить более простую структуру (схему), содержащую меньшее число состояний, элементов, но осуществляющую требуемые функции. Теоремы доказываются и используются в рамках формального логического базиса, определяемого совокупностью специальных правил. Логические методы представления систем относятся к детерминистским, хотя возможно их расширение в сторону вероятностных оценок. На базе математической логики созданы и развиваются теории логического анализа и логического синтеза, теория автоматов. На основе логических представлений первоначально начинали развиваться некоторые разделы теории формальных языков. В силу ограниченности смысловыражающих возможностей бинарной алгебры в последнее время имеются попытки создания многозначных алгебр логики с соответствующими логическими базисами и теоремами	Применяются при исследовании новых структур и систем разнообразной природы (технических объекта, текстов и др.), в которых характер взаимоотношений между элементами еще не настолько ясен, чтобы было возможно их представление аналитическими методами, а статистические исследования либо затруднены, либо не привели к выявлению устойчивых статистических закономерностей, В то же время следует иметь в виду, что с помощью логических алгоритмов можно описывать не любые отношения, а только те, которые предусмотрены законами алгебры логики и удовлетворяют требованиям логического базиса. Логические представления широко применяются при исследовании и разработке автоматов разного рода, автоматических систем контроля, при решении задач распознавания образов. На их основе развивается самостоятельный раздел теории формальных языков - языки моделирования проблемных ситуаций и текстов. В то же время смысловыражающие возможности логических методов ограничены базисом и не всегда позволяют адекватно отобразить реальную проблемную ситуацию.
Лингвистические		Основными понятиями, на которых базируются лингвистические представления, являются понятия: тезаурус Т, грамматика G, семантика, прагматика. Термин тезаурус (от греч. сокровищница, богатство, клад, запас и т. п.) в общем случае «совокупность научных знаний о явлениях и законах внешнего мира и духовной деятельности людей, накопленную всем человеческим обществом». В математической лингвистике и семиотике термин тезаурус используется в более узком смысле для характеристики конкретного языка, его многоуровневой структуры. Для этих целей удобно пользоваться одним из принятых в лингвистике определений тезауруса как «множества смысловыражающих элементов языка с заданными смысловыми отношениями, которое дал Ю.А. Шрейдер. Для системных приложений интересно сочетание математической лингвистики и семиотики, которая возникла как наука о знаках. Однако некоторые школы, развивающие семиотические представления, равноправно пользуются в семиотике понятиями математической лингвистики, такими как тезаурус, грамматика, семантика и т. п. Такие представления иногда называют лингвистической семиотикой или лингвосемиотикой.	Для практических приложении модели лингвистических и семиотических представлений можно рассматривать как один класс методов формализованного представления систем Лингвистические и семиотические представления возникли и развиваются в связи с потребностями анализа текстов и языков. Однако во второй половине XX в. эти представления стали широко применяться для отображения и анализа процессов в сложных системах в тех случаях, когда не удается применить сразу аналитические, статистические представления или методы формальной логики, В частности, лингвистические и семиотические представления являются удобным аппаратом (особенно в сочетании с графическими) для первого этапа постановки и формализации задач принятия решений в ситуациях с большой начальной неопределенностью, чем и был вызван интерес к этим методам со стороны инженеров и специалистов, занимающихся исследованием и разработкой сложных систем. На их основе разрабатывают языки моделирования и автоматизации проектирования.
		С теоретической точки зрения границу между лингвистическими и семиотическими представлениями при разработке языков моделирования можно определить характером правил грамматики: если правила не охватывается классификаций формальных грамматик Н. Хомсного, то модель относят к семиотической и применяют произвольные правила взаимоотношений между знаками, отображающими компоненты модели, допустимые семиотикой	При применении этих методов следует иметь в виду, что при усложнении языка моделирования, при применении правил произвольной грамматики или семиотики трудно гарантировать достоверность получаемых результатов, возникают проблемы алгоритмической разрешимости, парадоксов, которые частично могут быть преодолены с помощью содержательного контроля и корректировки языка на каждом шаге его расширения в диалоговом режиме моделирования
Графические		К графическим представлениям здесь отнесены любые графики (диаграммы, гистограммы, графики Гонта, т.е. «время-операция» в прямоугольных координатах и т д.) и возникшие на основе графических отображений теории: теорию графов, теорию сетевого планирования и управления и т, п., т. е. все, что позволяет наглядно представить процессы, происходящие в системах, и облегчить таким образом их анализ для человека (лица, принимающего решения). Есть и возникшие на основе графических представлений методы, которые позволяют ставить и решать вопросы оптимизации процессов организации, управления, проектирования и являются математическими методами в традиционном смысле. Таковы геометрия, теория графов. Понятие графа в математическом смысле первоначально было введено Л.Эйлером	Графические представления являются удобным средством исследования структур и процессов в сложных системах, средством организации взаимодействие человека и технических устройств (в том числе ЭВМ),

Для дискретных событий соотношение между возможными значениями случайной величины х, и их вероятностями р, называют законом распределения и либо записывают в виде ряда (таблице), либо представляют в виде зависимостей F(x)

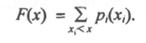
При этом

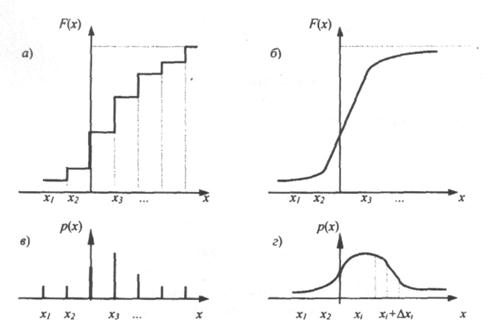
Рис. 2. Представление законов распределения

Для непрерывных случайных величин (процессов) закон распределения представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения - рис. 2, б), либо в виде плотности вероятностей (дифференциальный закон распределения - рис. 2, г). В этом случае где р(х) -вероятность попадания случайных событий в интервал от x до .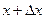

Для полной группы несовместных событий имеют место условия нормирования:

функции распределения

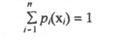
и плотности вероятности

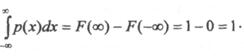
Закон распределения является удобной формой статистического отображения системы. Однако получение закона (даже одномерного) или определение изменений этого закона при прохождении через какие-либо устройства или среды представляет собой трудную, часто невыполнимую задачу. Поэтому в ряде случаев пользуются не распределением, а его характеристиками - начальными и центральными моментами.

Наибольшее применение получили:

1-й начальный момент - математическое ожидание или среднее значение случайной величины:

для дискретных величин,

для непрерывных величин;

2-й центральный момент - дисперсия случайной величины:для дискретных величин,

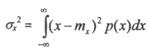
На практике иногда используется не дисперсия , а среднее квадратическое отклонение .

Связь между системами в общем случае характеризуется ковариацией — моментом связи; для двумерного распределения обозначаемых

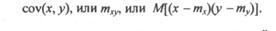
Можно использовать ковариацию нормированных отклонений - коэффициент кор­реляции

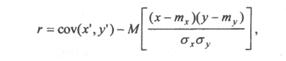
где , - нормированные отклонения; среднеквадратические отклонения.

Практическое применение получили в основном одномерные распределения, что связано со сложностью получения статистических закономерностей и доказательства адекватности их применения для конкретных приложений, которое базируется на понятии выборки.

Под выборкой понимается часть изучаемой совокупности явлений, на основе исследования которой получают статистические закономерности, присущие всей совокупно­сти и распространяемые на нее с какой-то вероятностью.

Для того чтобы полученные при исследовании выборки закономерности можно было распространить на всю совокупность, выборка должна быть представительной (репрезентативной), т. е. обладать определен­ными качественными и количественными характеристиками. Качественные характеристики связаны с содержательным аспектом выборки, т. е. с определением, являются ли элементы, входящие в выборку, элементами исследуемой совокупности, правильно ли отобраны эти элементы с точки зрения цели исследования (с этой точки зрения выборка может быть случайной, направленной или смешанной). Количественные характеристики представительности выборки связаны с определением объема выборки, достаточного для того, чтобы на основе ее исследования можно было делать выводы о совокупности в целом: уменьшение объема выборки можно

Теоретико-множественный подход в описании систем позволяет предложить следующую обобщенную модель (рис. 4.1, а)

Y = F: X

где:

Y={y₁,…,y_j,…,y_m} – выходная реакция системы;

X={x₁,…,x_j,…,x_n} – множество выходных воздействий;

F={F₁,…,F_j,…,F_m} – множество операторов, реализуемых системой.

Причем F_j 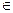F_R – множество физически реализуемых операторов с учетом необходимости соблюдения причинно-следственной связи

F_j(t,A): X(t,A) → y_j(t-t₀,A),

где: t₀ – задержка реакции системы Y на воздействие Х по времени t; А={α₁,…,α_k,…,α_s} – множество дестабилизирующих факторов, генерируемых множеством угроз Т, которому противостоит множество механизмов М защиты системы (рис. 3.1).

Иллюстрацией вполне может быть граф (рис. 4.1, а), где:

y_j=F_j(t,X)

и соответствующий ему (n+2)-местный предикат

Г(y_j,F_j,x₁,…,x_n)

или инцидентор на множествах

Г(Y,F,X).

Для информационных пространств СТС X,Y олицетворяют информационные ресурсы (концентраторы и хранители информации), а F - информационно-телекоммуникационные подсистемы (операторы обработки и передачи информации).

С учетом имеющей место задачи обеспечения безопасности системы имеем

Y = F: X (T 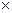M).

Тогда постановка этой задачи примет вид

,

где Y_э – множество эталонных значений выходной реакции Y системы;

Е₀ – множество порогов безопасности системы.

При этом могут быть сформулированы также определенные оптимизационные задачи:

- с точки зрения устойчивого функционирования системы;

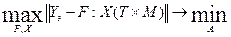
подсистемы защиты.

Для линейных систем (рис. 4.1,б) последние выражения не претерпят существенного изменения. В этом случае оператор F трансформируется в линейную передаточную функцию Н, где

y_j= , j=1(1)m.

При рассмотрении иерархически организованных систем (рис.4.2) m=1 или

y₀= .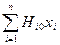

По формуле Мезона для типового звена иерархических систем имеем

y₀= ,

где: x_i – ресурс i-го компонента низшего уровня иерархии;

y₀ – ресурс высшего уровня иерархии;

k_i0 и k_0i – линейные операторы передачи между вышеупомянутыми ресурсами.

Глубина обратной связи для i-го компонента составит

1-L=1- k_i0k_0i,

а петлевая передача

L= k_i0k_0i.

Однако наиболее точную оценку степени защищенности системы возможно получить на основе исследования основного движения при воздействии дестабилизирующих факторов А

Y(t,A) = F(t,A): X(t,A).

Для этого уместно использовать функции чувствительности

S= - дифференциальной и

- относительной.

Рис. 4.1 Обобщенная структура системы

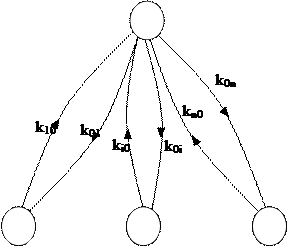
Рис 4.2. Типовое звено иерархических систем

Отсюда в первом приближении (без учета производных высшего порядка, что частенько допустимо при монотонной эволюции систем) имеем для дестабилизирующего фактора α_s и m=1 (иерархическая структура) следующее

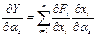
Осуществляя эквивалентные преобразования последнего выражения, при Y=∑F_i получаем

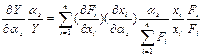или

.

Из данного выражения относительное отклонение для параметра Y будет равно

,

где = 1 – сумма коэффициентов вклада для каждого входа иерархической системы.

Поиск по сайту: