 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Разделение рисков на приемлемые и неприемлемые
Дополнительный способ оценивания рисков состоит в разделении их только на две категории: допустимые и недопустимые. Возможность применения подобного подхода основывается на том, что количественные показатели рисков используются только для того, чтобы их упорядочить и определить, какие действия необходимы в первую очередь. Но этого можно достичь и с меньшими затратами.
Таблица, используемая в данном подходе, содержит не числа, а только символы: Д – риск допустим и Н – риск недопустим (таблица 3).
Таблица 3 - Разделение рисков на допустимые и недопустимые.
| Показатель ресурса | Показатель частоты | ||||
| Д | Д | Д | Д | Н | |
| Д | Д | Д | Н | Н | |
| Д | Д | Н | Н | Н | |
| Д | Н | Н | Н | Н | |
| Н | Н | Н | Н | Н |
Следовательно, можно сделать вывод, что понятие риск имеет непосредственное отношение к ущербу как случайной величине, которая может быть как дискретной, так и непрерывной. Для непрерывного ущерба целесообразно воспользоваться плотностью распределения φ(u) (закон распределения вероятностей не имеет смысла) и интегральной функцией распределения
Φ(u)=  , причем
, причем  =1.
=1.
В этом случае нахождение вероятностей ущерба связано с вычислением соответствующих площадей (рис. 8.1). Так (рис. 8.1, а), вероятность непревышения ущерба заданной величины u1 находится следующим образом
P(u≤u1)= Φ(u1)=  ,
,
а вероятность превышения порога ущерба u2 будет равна (рис. 8.1, а)
P(u≥u2) = 1- Φ(u2)=  .
.
Вероятность попадания в заданный интервал ущерба (рис. 8.1, б) соответственно может быть найдена как разность
P(u1≤u≤u2)= Φ(u2)- Φ(u1)=  .
.
Исходя из вышеуказанных выражений, предлагается определить интегральные риски следующим образом:
Risk(u≤u1)=M(u≤u1) P(u≤u1)=M(u≤u1) Φ(u1);
Risk(u≥u2)=M(u≥u2) P(u≥u2)=M(u≥u2)[1- Φ(u2)];
Risk(u≤1u≤u2)=M(u1≤u≤u2) P(u1≤u≤u2)=M(u1≤u≤u2)[Φ(u2)- Φ(u1)],
где матожидания ущерба соответственно равны:
 | ||||||
|
|
U
Рис. 8.1. Плотность распределения ущерба
 | |||||
|  | ||||
Рис. 8.2. График для нахождения защищенности систем
 |
Рис. 8.3. Дискретизация плотности вероятности

Рис. 8.4 - Иллюстрация процесса нормировки плотности вероятности ущерба.

Рис. 8.5 - Дискретизация ущерба.

Рис. 8.6 - Наглядная иллюстрация процесса дискретизации риска.
M(u≤u1)=  ;
;
M(u≥u2)=  ;
;
M(u1≤u≤u2)=  .
.
Фактически интегральный риск предлагается рассматривать как произведение мат.ожидания ущерба (на рассматриваемом интервале) на вероятность попадания ущерба в интервал (функция интегрального распределения).
По аналогии интегральную защищенность системы в интервале ущерба можно определить отношениями (рис. 8.2):
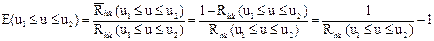 ;
;
 ;
;
 .
.
Возможен и усредненный риск, который уместно определить следующими выражениями
 ;
;
 ;
;
 .
.
Что же касается элементарного риска, то его распределение предлагается определить на основе дискретизации плотности распределения (рис. 8.2). Пусть (рис. 8.3, а) на отрезке [0,umax] области определения ущерба выбраны n дискрет uk, k=1(1)n с интервалом дискретизации Δu. Значения за границей umax (рис. 8.3, а) исключим из рассмотрения как запредельные, ограничившись оценкой вероятности катастрофы систем с помощью выражения
P(u>umax)=1-Ф(umax).
Тогда элементарный риск будет равен
risk(k)=ukPk(Δu)=uk[φ(uk)Δu],
где k=1(1)n. Нормируя по umax=nΔu, сводим рассмотрение в единичное пространство, т.е.
risk(k/n)=  .
.
Защищенность системы в этом случае можно определить по следующему выражению
 .
.
Подобная дискретизация открывает перспективу численной оценки по функции риска. Степень дискретизации определяет n, которое следует устанавливать исходя из условия квантования ущерба.
Характерно отметить, что предлагаемый подход имеет весьма широкую область практического приложения, ибо инвариантен к физической сущности описываемых процессов (от биологической безопасности в кардиологии до информационной безопасности в социотехнических системах). Здесь далее могут быть найдены для рисков соответствующие параметры случайной величины (мода, медиана, асимметрия и др.) с различными законами плотности распределения в контексте защищенности систем и их рисков.
Вместе с тем, уместно было бы аналитически определить основополагающие параметра риска (вероятности наступления ущерба определенной величины). Воспользуемся для этого рис. 8.3, б, откуда определим частные производные.
Максимум риска имеет место для ущерба величины u 0 при
φ'(u0)=0.
Максимальный рост (спад) риска имеет место для ущерба величин u 1 и u 2 при
φ''(u1)=φ''(u2)=0.
Зона повышенной опасности (повышенного риска) находится на отрезке: [ u 1, u 2].
В реальных системах имеет место необходимость учета нескольких возможных видов ущерба (по основным индикаторам состояния), для чего потребуется решение многомерной задачи и свертки к интегральному U.
Поиск по сайту: