 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Характеристики нечеткого множества
1.max  ) — максимум функции принадлежности.
) — максимум функции принадлежности.
2. α - уровневое множество:
· α - интерпретация как уверенности;
· диапазон разброса значение для уровневого множества;
· оценка упорядоченных значений с точки зрения «оптимизм — пессимизм»;
· Носитель нечеткого множества при α = 0: supp  .
.
3. Центр тяжести (ЦТ) функции принадлежности, обеспечивающей учет всего разброса значений. Определяется согласно следующего соотношения:
 (1.5)
(1.5)
Использование нечетких множеств предоставляет возможность представления с единых позиций различной информации:
· Четкой информации;
· Интервальной информации;
· Нечеткой информации, с модальность «возможно»
Нечеткие множества и распределение вероятности имеют между собой сходство и отличие
Нечеткие множества не тождественны распределению вероятностей, то есть  ≠Pr(x)
≠Pr(x)
Нечеткие множества могут быть преобразованы в распределения вероятности Рг и наоборот (при определенных условиях).
Рассмотрим наиболее часто встречающиеся трудности при использовании нечетких множеств для формализации плохо определенных данных.
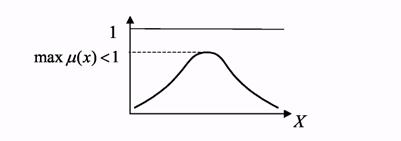
1. Не нормированное нечеткое множество max  < 1 (рис. 1.5).
< 1 (рис. 1.5).
При введении исходных данных и анализе полученных результатов требуется учет возможности отсутствия нормировки, что может быть обусловлено причинами, представленными в табл. 2. В этой же таблице представлены возможные варианты выхода из сложившейся трудности.
Таблица 2 — Причины отсутствия нормировки нечетких множеств и возможные подходы к учету этого
| Причина | Возможный выход |
| Отсутствие полного определения множества | Ведение фиктивного элемента (блока) во множество X |
| Модальность распределения нечеткости | Проведение исследований с использованием нечетких мер |
| Получение ненормированного нечеткого множества вследствие результата выполненной операции | Выполнение процедуры нормализации (имеются проблемы нелинейного преобразования и, следовательно, сложности интерпретации) или использование полученного результата с учетом отсутствия нормировки. |
|
Рисунок 1.5 - Не нормированное нечеткое множество
2. Многомодовость нечеткого множества.
Многомодовость нечеткого множества обуславливается данными, имеющими «сгустки» распределения уверенности. Например, в оценках типа (Рис. 1.6):
«Может быть 10, а может быть и 15, но с меньшей степенью уверенности»
При обработки подобных данных возникают неоднозначности решений, что затрудняет как алгоритмизацию вычислительных процедур, так и интерпретацию получаемых решений.
• Вариантами решения проблемы является:
a) Разбитие многомодового нечеткого множества на отдельные моды (Рис. 1.6);
b) Построение «выпуклой оболочки» многомодового нечеткого множества (Рис. 1.6);
c) Использование полученного результата с учетом его многомодовости.

Рисунок 1.6 — Представление многомодового нечеткого множества
3. Ошибка центра масс нечеткого множества
Трудность обусловлена тем, что при смещении мало значащих значений в сторону больших значений X (рис. 17, при упорядоченном X, в частности при использовании нечетких чисел) наблюдается смещение центра масс нечеткого множества, что приводит к ошибкам интерпретации значения нечеткого множества.

Рисунок 1.7 — Пример смещения центра масс при учете малозначащих значений
Возможным вариантом устранения погрешностей является использование подходов α-уровневой фильтрации («отсечение» значений с функцией принадлежности меньше α, см. рис. 1.7).
4. Сложности определения нечеткого множества для сложных понятий
Проблема обусловлена возникновением естественных трудностей для специалиста, который должен определить нечеткие оценки для сложного понятия. Данные трудности связаны с трудностями психологического шкалирования.
Операции над нечеткими множествами
В настоящее время разработано достаточно большое количество операций над нечеткими множествами. Ниже в таблице приведены ссылки на основные, наиболее часто используемые операции над нечеткими множествами.
Таблица 3 - Наиболее часто используемые операции над нечеткими множествами.
| № | Наименование операции | Интерпретация | Возможные трудности |
| 1 | Операция объединения | Операция «ИЛИ». Надо чтобы выполнялось хотя бы одно условие | Появление многомодовости получаемых результатов |
| 2 | Операция пересечения | Операция «И». Надо чтобы выполнялись все условия | Уменьшение максимального значения max  и
появление не нормированных нечетких множеств и
появление не нормированных нечетких множеств
|
| 3 | Операция Сжатия-растяжения | Уточнение, проявление уровня уверенности в оценках. | Необходимо учитывать нелинейный характер преобразований. |
| 4 | Импликация (эквивалентн ость) | Операция следования или связи на уровне сравнения объектов | При решении практических задач требует выбора конкретного типа данной операции в соответствии с физикой моделируемого объекта |
| 5 | Операция отрицания | Оценка противоположного события. | Зависит от выбранного генератора отрицания и требует выбора конкретного типа отрицания в соответствии с физикой моделируемого объекта |
| 6 | ┴иТ- нормы и конормы, Средние, OWA-оператор | Могут выполнять различную логику обработки данных в зависимости от выбранных параметров операторов | При решении практических задач требует выбора конкретного типа данной операции в соответствии с физикой моделируемого объекта |
Проблема определения операции агрегирования нечетких множеств определяется теми же проблемами, которые отмечены Для получения адекватных оценок необходимо осуществлять процедуры идентификации операций над нечеткими множествами для реальных моделируемых процессов.
Рассмотрим индекс нечеткости или показатель размытости нечетких множеств.
Если объект х обладает свойством R (порождающим нечеткое множество A) лишь в частной мере, т.е. 0 <mA(x) <1, то внутренняя неопределенность, двусмысленность объекта х в отношении R проявляется в том, что он, хотя и в разной степени, принадлежит сразу двум противоположным классам: классу объектов, "обладающих свойством R ", и классу объектов, "не обладающих свойством R ". Эта двусмысленность максимальна, когда степени принадлежности объекта обеим классам равны, т.е. mA (x) =  (x)=0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо mA (x) = 1 и
(x)=0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо mA (x) = 1 и  (x) = 0, либо mA (x) = 0 и
(x) = 0, либо mA (x) = 0 и  (x) = 1.
(x) = 1.
В общем случае показатель размытости нечеткого множества можно определить в виде функционала d(A) со значениями в R (положительная полуось), удовлетворяющего условиям:
1. d(A) = 0 тогда и только тогда, когда А - обычное множество;
2. d(A) максимально тогда и только тогда, когда mA (x) = 0.5 для всех xÎE.
3. d(A)d(B), если A является заострением B, т.е.
4. mA (x) £mB (x) при mB (x) < 0,5;
5. mA (x) ³mB (x) при mB (x) > 0,5;
6. mA (x)- любое при mB (x) = 0,5.
7. d(A) = d (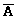 ) - симметричность по отношению к 0,5.
) - симметричность по отношению к 0,5.
8. d(AÈB)+d(AÇB) = d(A)+d(B).
Обычное множество, ближайшее к нечеткому
Пусть A - нечеткое множество. Возникает вопрос, какое множество A ÌE является ближайшим к A, т.е. находится на наименьшем евклидовом расстоянии от нечеткого множества A. Таким подмножеством, обозначаемым A, является подмножеством с характеристической функцией:
 . (1.6)
. (1.6)
Обычно принимают mA (xi) = 0, если mA (xi) = 0,5.
Используя понятие обычного множества, ближайшего к нечеткому, введем следующие индексы нечеткости нечеткого множества А.
Линейный индекс нечеткости:

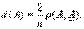
Здесь r(A, A) - линейное (хеммингово) расстояние, множитель - обеспечивает выполнение условия 0 < d(A) < 1.
Поиск по сайту: