Лекция 3. Математическое описание «системы»

Ранее было установлено, что система представляет собой множество элементов, объединенных в целое за счет взаимодействия элементов друг с другом, т.е. за счет отношений между ними, и обеспечивает преимущества в достижении целей. Преимущества в достижении целей обеспечиваются за счет системного эффекта. Системный эффект состоит в том, что свойства системы не сводятся к сумме свойств ее элементов, т.е. система как целое обладает рядом новых, т.е. эмерджентных свойств, которых не было у ее элементов. Уровень системности тем выше, чем выше интенсивность взаимодействия элементов системы друг с другом, чем сильнее отличаются свойства системы от свойств входящих в нее элементов, т.е. чем выше системный эффект, чем значительнее отличается система от множества. Элементы взаимодействуют (вступают в отношения) друг с другом с помощью имеющихся у них общих свойств, а также свойств, которые коррелируют между собой.

Таким образом, система обеспечивает тем большие преимущества в достижении целей, чем выше ее уровень системности. В частности, система с нулевым уровнем системности вообще ничем не отличается от множества образующих ее элементов, т.е. тождественна этому множеству и никаких преимуществ в достижении целей не обеспечивает. Этим самым достигается выполнение принципа соответствия между понятиями системы и множества. Из соблюдения этого принципа для понятий множества и системы следует и его соблюдение для понятий, основанных на теории множеств и их системных обобщений.

Рассмотрим системное обобщение самой теории множеств и преобразования ее в математическую теорию систем, которая будет плавно переходить в современную теорию множеств при уровне системности, стремящемся к нулю. При этом необходимо заметить, что существующая в настоящее время наука под названием "Теория систем" ни в коей мере не является обобщением математической теории множеств, и ее не следует путать с математической теорией систем.

Общие понятия теории систем

Общая система, глобальные состояния и глобальная реакция системы

При построении теории общих систем мы будем исходить из следующих определений.

(Общей) системой называется отношение на непустых (абстрактных) множествах

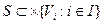(1.1)

где 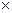символ декартова произведения, а I – множество индексов. Множество V_i мы будем называть объектом системы. Если множество I конечно, то (1.1) можно переписать в виде

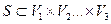(1.2)

Пусть 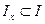и образуют разбиение множества I, т. е. пусть 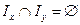и .. Множество 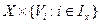будем называть входным объектом, а множество- 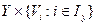выходным объектом системы. Тогда система S определяется отношением

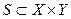(1.3)

(такую систему мы будем называть системой «вход — выход»)).

Если S является функцией

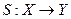(1.4)

то соответствующая система будет называться функциональной.

Заметим, что в формулах (1.2) и (1.3) используется один и тот же символ S, хотя, строго говоря, элементами отношения в (1.2) являются n-ки, в то время как в (1.3) — это пары. Конкретный характер интерпретации S всегда будет ясен из контекста, в котором этот символ используется. Аналогичные замечания можно высказать и по поводу использования одинакового символа S в (1.3) и в (1.4).

Для удобства обозначений мы примем также следующее соглашение: скобки в
выражении 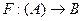будут означать, что функция F является всего лишь частичной, т.е. что она не обязательно определена для любого элемента множества А. Область пределения функции F (или просто область) будет обозначаться через 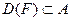, а область ее значений(или ее кообласть)

через 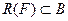. Аналогично будут обозначаться и область, и кообласть отношения :

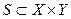и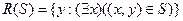

Для упрощения обозначений в дальнейшем всегда будет предполагаться, что D(S) = X, если только не оговорено противное.

Для данной общей системы S пусть С произвольное множество, а функция 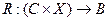такова, что

Тогда С называется множеством или объектом глобальных состояний системы, а его элементы – просто глобальными состояниями системы, функция же R называется глобальной реакцией (системы).

Теорема 1.1. Каждой системе соответствует некоторая глобальная реакция, и эта функция R не является частичной, т. е.

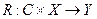
Поиск по сайту: