АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Эллипс. Каноническое уравнение эллипса и его свойства

Читайте также:
  1. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  2. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  3. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  4. Волна вероятности. Уравнение Шредингера
  5. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  6. Временное и стационарное уравнение Шредингера. Решения.
  7. Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля
  8. Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.
  9. Гипербола. Каноническое уравнение гиперболы и его свойства.
  10. Давление газа с точки зрения молекулярно-кинетической теории. Уравнение состояния идеального газа.
  11. Давление газа. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Изопроцессы.
  12. Деньги и денежные агрегаты. Уравнение обмена. Спрос и предложение на рынке денег.

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которой до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая,чем расстояние между фокусами

MF1+MF2=2a

каноническое уравнение эллипса:

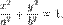
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.

Эллипс-кривая второго порядка.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника

3) Эксцентриситет эллипса e < 1.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)