АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки»

Читайте также:
  1. Але монетарне правило не враховує мінливості швидкості обігу грошей та чутливості попиту до зміни процентної ставки.
  2. Б) Если основной определитель системы равен нулю и хотя бы один из вспомогательных определителей не равен нулю, то система – несовместна.
  3. В прошлом году российские операторы сотовой связи получили лицензии на предоставление услуг связи третьего поколения. Но это- лишь первый шаг к построению мобильной сети 3G.
  4. В чем особенности компьютеров третьего поколения?
  5. Виды НКО и концепции третьего сектора
  6. Виды светофоров и правило их установки
  7. Вопрос№10 Явление электромагнитной индукции. Правило Ленца
  8. Второе правило
  9. Глава 13. Валютно-финансовые отношения в начале третьего тысячелетия 377
  10. Глава 13. Валютно-финансовые отношения в начале третьего тысячелетия 403
  11. Глава 13. Валютно-финансовые отношения в начале третьего тысячелетня 375
  12. Глава VI. Правило фаз.

Определителем матрицы называется некоторая математическая функция элементов квадратной матрицы, результатом которой является число.
Обозначение:
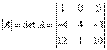— определитель 3- го порядка (т.к. матрица размера 3 на 3) матрицы А.
Замечание: В этом, якобы простом, определении определителя (звучит как тавтология) говориться, что с элементами матрицы нужно что то сделать (умножить, сложить, разделить и т.д.) и получится значение определителя этой матрицы. Однако не сказано. Что же все-таки надо с ними сделать.

Вычисление определителей первого порядка.
Матрица размера 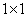это просто число. Определителем такой матрицы является само это число.
Вычисление определителей второго порядка.
Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:

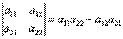
Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.
Пример:
.

 
 

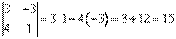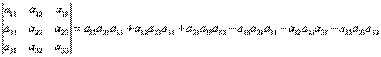Вычисление определителей третьего порядка.
 Определитель третьего порядка вычисляется по правилу:
Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников:

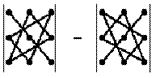
Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":




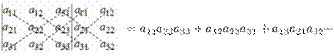
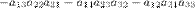
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)