АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Общее уравнение прямой на плоскости в представлении геометрических векторов

Читайте также:
  1. A) общее собрание акционеров
  2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  3. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  4. В клинической практике выделяют различные формы афазий, дизартрии, алалию, мутизм и общее недоразвитие речи.
  5. В отделение проктологии поступил больной с жалобами на кровотечение из стенок прямой кишки.
  6. В результате получаем общее решение системы
  7. Векторы на плоскости
  8. ВЛАСТЬ И ВЛИЯНИЕ. ОБЩЕЕ ПОНЯТИЕ. ИСТОЧНИКИ ВЛАСТИ В ОРГАНИЗАЦИИ. ЛИДЕРСТВО И ВЛАСТЬ
  9. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  10. Волна вероятности. Уравнение Шредингера
  11. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  12. Вопрос 1 Корреляционные функции и спектральные плоскости.

Ax+By+C=0

A,B,C – произвольные числа, причем А и В не равны нулю одновременно.

· Если В=0, то уравнение имеет вид Ax+C=0, А≠0, т.е. . Это есть уравнениепрямой, параллельной оси Oyи проходящей через точку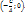

· Если В≠0, то из уравнение получаем . Это есть уравнение прямой с угловым коэффициентом

.

Некоторые частные случаи общего уравнения прямой:

1) Если А=0, то уравнение приводится к виду . Это есть уравнение прямой, параллельной оси Ох;

2) Если В=0, то прямая параллельна оси Оу;

3) Если С=0, то получаем Ах+Ву=0. Уравнению удовлетворяют координаты точки О(0;0), прямая проходит через начало координат.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)