АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Векторы на плоскости

Читайте также:
  1. Векторы и ориентиры современной культурологии
  2. Векторы и скаляры
  3. Векторы.
  4. Вопрос 1 Корреляционные функции и спектральные плоскости.
  5. Вопрос27 Полярная и декартова системы координат на плоскости. Связь между полярными и декартовым системами координат. Цилиндрические и сферические системы координат на плоскости.
  6. Восприятие точки, линии, пятна на плоскости
  7. ВОСПРИЯТИЕ ФОРМЫ НА ПЛОСКОСТИ
  8. Вращение плоскости поляризации
  9. Вращение плоскости поляризации
  10. Вращение плоскости поляризации. Оптически активные вещества. Удельное вращение. Поляриметрия (сахариметрия)
  11. Геометрические векторы.

Определение1: Вектором называется направленный отрезок.

Обозначается латинскими буквами со стрелкой наверху: .

Вектор, заданный парой (А, В) несовпадающих точек, обозначается символом . Точка А называется началом, а точка В – концом вектора.

Определение2: Д линой (модулем) вектора называется расстояние между его началом и концом.

Обозначается . Вектор , концы которого совпадают, называется нулевым вектором.

Пусть А 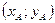, В Длина вектора находится по формуле .

Определение3: Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается символом . Таким образом, по определению,

.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)