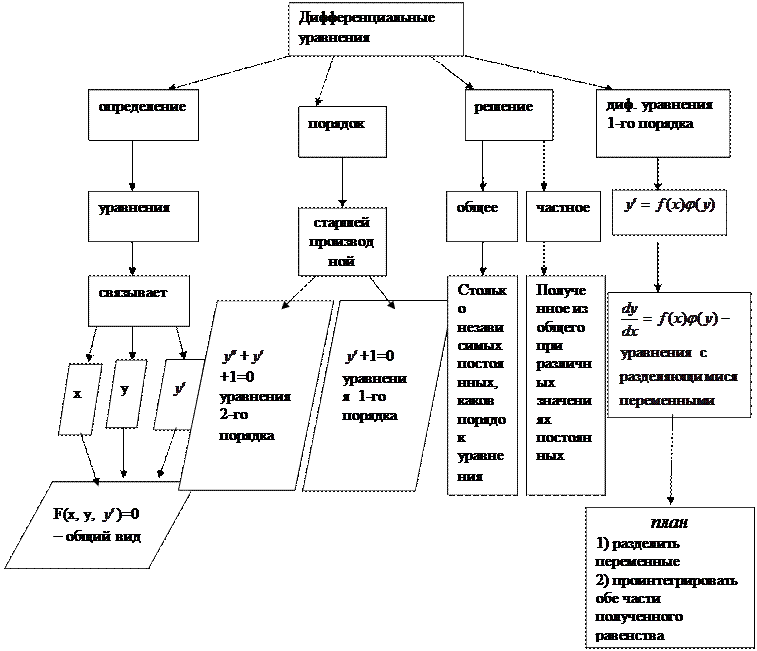
Дифференциальные уравнения первого порядка с разделяющимися переменными

Определение: Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию у и ее производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Определение: Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

Определение: Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

Определение: Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.

Определение: Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.

Определение: Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы)не выше первого порядка.

Определение: Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

.

Для решения этого уравнения нужно сначала разделить переменные:

а затем проинтегрировать обе части полученного равенства:

Поиск по сайту: