АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах

Читайте также:
  1. V – скорость буксировки, м/с.
  2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  3. Алекс с таким удовольствием начал рассказывать, поясняя смысл текстов, что совсем забылся.
  4. Анализ времён распространения гаплогруппы R1b1a2
  5. Анализ различных критериев периодизации психического развития. Понятие ведущей деятельности
  6. Атмосфера марша была торжественной. Клив Джонс чувствовал воодушевление. Все эти месяцы ему было так одиноко. Но вот - здесь тысячи людей, и среди них нет безразличных.
  7. Бессмысленное истощение земель
  8. Билет № 17 Философский смысл эпохи просвещения
  9. Биологический смысл основных религиозных понятий. Краткий словарь
  10. Биологический смысл основных религиозных понятий. Краткий словарь.
  11. Будущее бессмысленно
  12. Бытовой уровень. Что такое счастье и смысл жизни

Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид

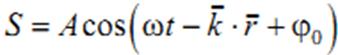
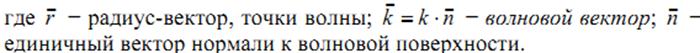
Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности. Перейдем от радиус-вектора точки к ее координатам x, y, z.

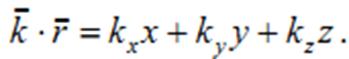
Тогда уравнение (6.3.1) примет вид

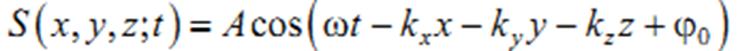
Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)

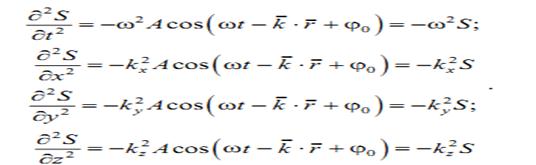
Сложив производные по координатам, и с учетом производной по времени, получим

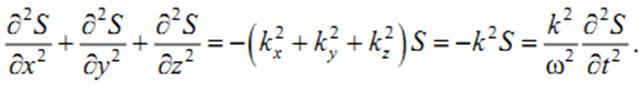
Произведем замену

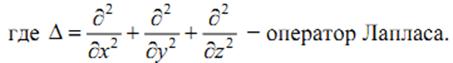
И получим волновое уравнение


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)