Момент инерции МТ и АТТ. Теорема Штейнера. Расчет момента инерции тонкого стержня

момент инерции АТТ отн. оси вращ. Z.

: момент инерции МТ отн.оси.

Физ.смысл: момент инерции тела явл. Мерой инертности тела при его вращательном движении, причём момент инертности любой оси характеризует его независимо от того, покоится тело или движется.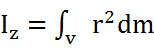

Свойства момента инерции:

1. Теорема Штейнера:

2. Правило сложения: момент инерции системы отн.некоторой оси=сумме моментов инерций частей этой системы отн.этой же оси.

Расчёт момента инерции системы тонкого стержня:

Момент инерции тонкого стержня отн.оси АА’, проходящей через середину. Длина-l, масса-m.

1. Разделим на малые элементы длины dx с массой на расстояние x от оси. Момент инерции элемента:

2. Интегрируем в пределах от 0 до и удваиваем:

Вопрос 25 Работа при вращательном движении. Кинетическая энергия вращения МТ, системы МТ, АТТ вокруг оси. Полная кинетическая энергия АТТ. Закон изменения кинетической энергии при вращательном движении.

Работа, совершаемая всеми приложенными к телу силами, идет

на изменение его кинетической энергии: δA = dК. Подставим в последнее выражение уравнение (4.9.3 см. ниже) и продифференцируем , учитывая, что , получим: Тогда элементарная работа, совершаемая силами, приложенными к телу: и полная работа при повороте тела на угол φ за время t:
Линейная скорость элементарной массы m_i равна υ_i = ωR_i, где R_i − расстояние от элементарной массы до оси вращения. Кинетическая энергия этой элементарной массы получается выражением
. Кинетическая энергия тела складывается из кинетических энергий его частей, т.е. . Так как величина есть момент инерции тела относительно оси вращения, то кинетическая энергия тела, вращающегося вокруг неподвижной оси (4.9.3)!!!

Кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс, и энергии вращения вокруг оси, проходящей через центр масс тела, т. е.

Поиск по сайту: