 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема сложения скоростей в СТО
Формула преобразования скоростей вСТО устанавливает связь между проекциями скорости точки в двух произвольных инерциальных системах отсчета. Пусть в системах отсчета 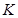 и
и  движение МТ определяется координатным способом
движение МТ определяется координатным способом
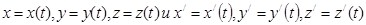
Тогда проекции скоростей
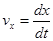 ,
, 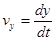 ,
, 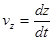 и
и 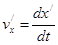 ,
, 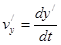 ,
, 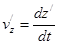
Воспользуемся преобразованием Лоренца и продифференцируем
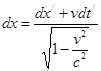 ,
, 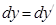 ,
, 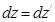 ,
, 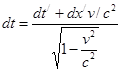 и получим
и получим
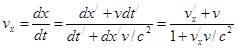 (1)
(1)
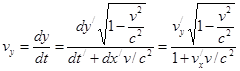 (2)
(2)
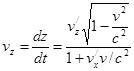 (3)
(3)
Выражения 1-3 являются формулами преобразования скоростей при переходе от одной системы отсчета в другую(релятивистский закон сложения скоростей).
Если аналогичные действия проделать с обратными преобразованиями Лоренца, то получим выражение для скоростей в системе  скоростей в системе
скоростей в системе 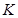 .
.
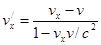 ,
, 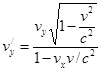 ,
, 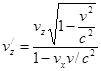 .
.
Поиск по сайту: