Временное и стационарное уравнение Шредингера. Решения

Общее уравнение Шредингера называют также уравнением Шредингера, зависящим от времени. Оно является основным уравнением нерелятивистской квантовой механики. уравнение должно быть уравнением относительно волновой функцией Ψ(х, у, z, t). Также это уравнение должно обладать некоторыми чертами, присущими волновому уравнению для упругих волн, поскольку оно призвано учитывать волновые свойства микрочастиц.

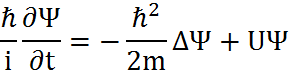
Стационарное уравнение Шредингера.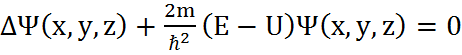

Функции 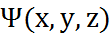, являющиеся решениями уравнения, называются собственными функциями. Уравнения в ряде случаев имеют решения не при всех значениях энергии Е, а лишь при определенных ее значениях. Значения энергии Е, при которых имеет место решение уравнения Шредингера, называют собственными значениями энергии. Собственные значения энергии Е могут образовывать как не-прерывный, так и дискретный ряд значений энергии. В первом случае говорят о непрерывном, во втором − о дискретном спектре энергии.

Поиск по сайту: