АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Предмет квантовой механики. Волновая функция, ее свойства и статистический смысл

Читайте также:
  1. I. Предмет и метод теоретической экономики
  2. I.ПРЕДМЕТ ДОГОВОРА
  3. III. Предмет, метод и функции философии.
  4. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  5. Алгебраические свойства векторного произведения
  6. АЛГОРИТМ И ЕГО СВОЙСТВА
  7. АТМОСФЕРА И ЕЕ СВОЙСТВА
  8. Атрибуты и свойства материи
  9. Базовые понятия предметного поля социальной информатики
  10. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
  11. Билет 1. Предмет истории как науки: цели и задачи ее изучения
  12. Билет 12. Предмет социальной философии. Уровни анализа общественных отношений

1. Первый постулат квантовой механики

Движение микрочастиц в пространстве имеет вероятный (стохастастический) хар-тер

Согласно корпускулярно-волновому дуализму состав микрочастиц можно было бы описывать волновыми образованиями, занимающее все пространство или его небольшие части в виде волн. пакета.

2. Второй постулат квантовой механики

Математический формализм кв. мех. описывает состав микрочастиц заданной волновой функцией.

(ВФ)-

Квадрат амплитуды световой волны определяет плотность вероятности попадания фотона в соответствующую точку пространства.

- постулат Борна

Квадрат модуля комплексной волновой функции определяется соотношением

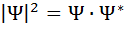- статистическая, т. е. вероятностная, интерпретация квадрата модуля волновой функции.

Вероятность обнаружения частицу в объеме

2

2

Вероятность обнаружения частицы в , где – это шар радиуса

2

Свойства :

1) Должна быть конечной (вероятность не может быть больше 1), однозначной (вероятность не может быть неоднознач.) и непрерывной(вероятность не может быть изменена скачком)

2) произведение – должно быть непрерывным

3) принцип суперпозиций – если физ. величина может находиться в сост. , то

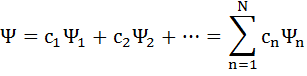
4) Должна быть интегрируема – это условие сводится к условию нормировки вероятностей. Вероятность найти частицу где-нибудь в объеме :

2

5) Вид ф-ции находится с помощью с помощью решения спец. дифференциального ур-ния – ур-ния Шредингера


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)