 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгоритм расчета дисперсионных характеристик плоского трехслойного оптического волновода
Рассмотрим алгоритм расчета дисперсионных характеристик плоского трехслойного оптического волновода на примере TE-мод.
На первом этапе при выбранных параметрах 
и 
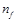путем численного решения уравнения (21) определяются нормированные частоты отсечек 
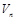. Для решения уравнения (21) может использоваться любой итерационный метод нахождения корней (метод бисекции, метод хорд, метод секущих и т.д.). Уравнение (21) имеет бесконечное число корней 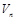, каждый из которых определяет частоту отсечки TE-моды с индексом 
(порядковый номер корня). Самый минимальный по значению корень соответствует частоте отсечки нулевой (основной) TE-моды.
На втором этапе при различных значениях нормированной частоты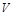 
численно решается уравнение (19) и определяются его корни 
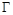. Расчет необходимо начинать с нормированной частоты 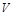, равной частоте отсечки нулевой моды 
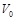, которая была рассчитана на первом этапе. Очевидно, что при 
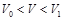уравнение (19) будет иметь один корень, соответствующий нормированной постоянной распространения нулевой TE-моды. При 
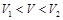уравнение (19) будет иметь уже два корня, больший по значению из которых соответствует нулевой моде, а меньший — первой. При 
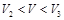уравнение (19) будет иметь три корня и т.д.
Таким образом, для каждой частоты 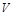путем численного решения уравнения (19) определяется набор корней 
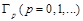, каждый из которых соответствует собственной волне 
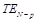(N — общее число корней на частоте). В результате строится график функции 
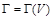, которая имеет несколько ветвей, соответствующих различным собственным волнам.
Примерный вид дисперсионной характеристики представлен на рис.2. По оси абсцисс отложены значения нормированной частоты 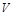, а по оси ординат — соответствующие им значения нормированной постоянной распространения 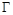. Кружками отмечены частоты отсечек собственных волн.
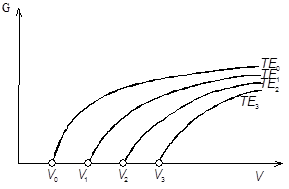
Рисунок 2. Типичный вид дисперсионной характеристики
Для построения дисперсионных характеристик TM-мод необходимо численно решать уравнение (22), предварительно перейдя в нем к нормированным переменным. Частоты отсечек TM-мод определяются путем решения уравнения (23). Алгоритм расчета дисперсионных характеристик TM-мод плоского трехслойного оптического волновода аналогичен рассмотренному выше случаю TE-мод.
Ниже рассматриваются возможности программы MathCad для расчета дисперсионных характеристик плоских оптических волноводов в автоматическом режиме.
Поиск по сайту: