Упражнение 2. Исследование дисперсионных характеристик плоского оптического волновода с профилем показателя преломления световедущей пленки изменяющимся по параболическому закону

Геометрия оптического волновода показана на рисунке 2.

Для выполнения упражнения выберите в выпадающем списке значение Параболический профиль.

1. Для указанных параметров геометрии задачи (см. таблицу) построить дисперсионные характеристики (зависимости ) для первых четырех типов мод. Определить по графикам частоты отсечек данных мод и найти частотный диапазон одноволновости (интервал между частотами отсечек нулевой и первой мод).

2. Построить зависимость показателя преломления от поперечной координаты. (Для этого нажмите кнопку Просмотр профиля.)

3. Построить распределения полей первых четырех типов мод. (Для этого нажмите кнопку Поле.)

Отчет должен содержать четыре графика, отображающие дисперсионные характеристики для указанных типов собственных волн, значения частот отсечек и величину диапазона одноволновости. Необходимо построить распределения полей вдоль поперечной координаты 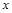для мод с индексами .

Рисунок 2

Упражнение 3. Исследование дисперсионных характеристик плоского оптического волновода с профилем показателя преломления световедущей пленки изменяющимся по закону 1/ch²(x).

Геометрия оптического волновода показана на рисунке 3.

Для выполнения упражнения выберите в выпадающем списке значение Профиль по закону 1/( ch(x))^2.

1. Для указанных параметров геометрии задачи (см. таблицу) построить дисперсионные характеристики (зависимости ) для первых четырех типов мод. Определить по графикам частоты отсечек данных мод и найти частотный диапазон одноволновости (интервал между частотами отсечек нулевой и первой мод).

2. Построить зависимость показателя преломления от поперечной координаты. (Для этого нажмите кнопку Просмотр профиля.)

3. Построить распределения полей первых четырех типов мод. (Для этого нажмите кнопку Поле.)

Отчет должен содержать четыре графика, отображающие дисперсионные характеристики для указанных типов собственных волн, значения частот отсечек и величину диапазона одноволновости. Необходимо построить распределения полей вдоль поперечной координаты 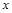для мод с индексами .

Значения других параметров, используемых при расчетах:

Нормированная частота — предел расчета дисперсионных характеристик по частоте V:

.

Число точек кривой — число точек по нормированной частоте V, в которых производится расчет:

Рисунок 3

ОПИСАНИЕ РАБОТЫ С ПРОГРАММОЙ «Labwork».

Интерфейс программы:

Рисунок 4. Интерфейс программы

1 — Выбор типа поляризации собственной волны

2 — Предел изменения частоты световой волны

3 — Выбор номера моды

4 — Показатель преломления световедущей пленки

5 — Показатель преломления подложки

6 — Показатель преломления покровного слоя

7 — Величина параметра асимметрии волноведущей структуры

8 — Список, отображающий значения нормированных частот V (1 столбец) и соответствующих им постоянных распространения b (2 столбец). Используя данные этого списка производится построение дисперсионных характеристик.

9 — Выбор профиля показателя преломления волноведущей пленки:

Рисунок5. Выбор вида профиля показателя преломления

10 — Кнопка РАСЧЕТ. При нажатии происходит расчет дисперсионной характеристики при заданных параметрах и полученные значения выводятся в список 8.

11 — Кнопка ПРОСМОТР ПРОФИЛЯ. При нажатии на экране монитора отображается график, определяющий зависимость показателя преломления от поперечной координаты .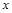

Рисунок 6. Пример профиля показателя преломления

12 — Кнопка ПОЛЕ. При нажатии на экране отображается график, иллюстрирующий зависимость компоненты электрического поля 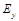от поперечной координаты 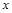для заданного профиля показателя преломления и выбранной моды.

Рисунок 7. Пример распределения электрического поля моды

СВЕДЕНИЯ ИЗ ТЕОРИИ ПЛОСКИХ ОПТИЧЕСКИХ ВОЛНОВОДОВ

1. Плоский трехслойный волновод с постоянной величиной
показателя преломления световедущей пленки

В предлагаемой лабораторной работе производится электродинамический анализ плоского трехслойного диэлектрического оптического волновода (световод показан на рисунке 8).

Рассматриваемая структура состоит из трех диэлектрических слоев: волноведущей пленки с показателем преломления 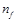, покровного слоя () и подложки (). Для устранения межмодовой дисперсии пленка может иметь плавно изменяющийся показатель преломления . Согласно лучевой теории, в этом случае различные моды, имеющие неодинаковые фазовые скорости будут испытывать различные по величине рефракционные искривления траектории луча.

Рисунок 8

Для возможности канализации излучения в центральном слое необходимо выполнение условия: . В этом случае световая волна будет распространяться вдоль волноведущей пленки путем переотражений от границ раздела «пленка-покровный слой» и «пленка-подложка», где будет выполняться условие полного внутреннего отражения. Различные углы переотражений будут соответствовать различным типам собственных волн (модам). При этом необходимо выполнение условия фазового согласования:

(1)

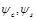где — толщина волноведущей пленки, — угол переотражения, — сдвиги фаз при отражении световой волны от покровного слоя и подложки соответственно, — индекс, определяющий порядковый номер моды.

Из приведенного соотношения следует вывод, что в рассматриваемой световедущей структуре возможно распространение бесконечного числа мод, обладающих дискретными углами переотражения .

В интегральной оптике принято при построении дисперсионных характеристик переходить к безразмерным нормированным величинам, аналогам волнового числа 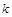и постоянной распространения 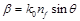( 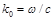— волновое число для вакуума). Обычно используют три нормированных параметра:

— эффективный волноводный показатель преломления;

— нормированная частота;

— нормированный эффективный волноводный показатель преломления.

Для описания степени несимметрии показателей преломления подложки и покровного слоя вводят параметр асимметрии:

. (2)

В результате введения нормированных параметров дисперсионное уравнение для плоского трехслойного оптического волновода для случая неизменного показателя преломления волноведущей пленки имеет вид:

(3)

Частоты отсечек такого волновода определяются из соотношения:

(4)

2. Плоский трехслойный волновод с показателем преломления
световедущей пленки, изменяющимся по параболическому закону.

Некоторые технологические процессы, такие как диффузия и ионная имплантация, приводят к тому, что волноведущий слой оптического волновода имеет показатель преломления, который плавно изменяется вдоль некоторого поперечного направления. Такая структура обеспечивает периодическую фокусировку светового пучка в центральной (осевой) части волновода.

Одним из примеров такого плавноизменяющегося профиля является квадратичная среда (профиль соответствующий ей называется параболическим). Зависимость диэлектрической проницаемость световедущего слоя от координаты 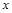имеет вид:

(5)

где 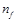— максимальное значение показателя преломления в центре волновода; .

В этом случае зависимость нормированного эффективного показателя преломления от волнового числа 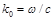( — круговая частота; — скорость света) имеет вид:

(6)

Переходя к нормированной частоте 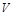, приходим к следующему дисперсионному уравнению:

(7)

Частоты отсечек определяются из выражения:

(8)

3. Плоский трехслойный волновод с показателем преломления световедущей пленки, изменяющимся по закону 1/ch²(x).

Закон изменения показателя преломления в данном случае имеет вид:

(9)

В этом случае зависимость нормированного эффективного показателя преломления от волнового числа 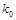имеет вид:

(10)

где

Дисперсионное уравнение в нормированных величинах может быть записано в следующем виде:

(11)

Частоты отсечек определяются из соотношения:

(12)

Поиск по сайту: