Упражнение 2. Расчет дисперсионных характеристик собственных волн плоского трехслойного оптического волновода

Для указанных параметров необходимо рассчитать нормированные дисперсионные характеристики четырех низших TE или TM-мод(в зависимости от варианта задания). Для TE-мод дисперсионные уравнения имеют вид (20), для TM-мод — (22).

Рассмотрим алгоритм на примере TE-мод. Путем численного решения уравнения (20) определяются все корни Г на фиксированной частоте V.

1. Производим ввод параметров волновода.Должны быть заданы показатели преломления слоев nf, nc, ns и относительные диэлектрические проницаемости ef, ec, es. Кроме того, необходимо задать значение нормированной частоты V. Отметим, что V не может быть меньше, чем (нормированная частота отсечки нулевой моды), которая была определена в упражнении 1.

2. Зададим функцию, равную левой части уравнения (20), корни которого мы собираемся определять:

Здесь переменная x выступает в качестве нормированной постоянной распространения Г.

Обратим внимание, что условием распространения электромагнитной волны в волноводе является условие:

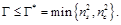
В противном случае подкоренное выражение оказывается отрицательным, а волна становится затухающей.

Для нахождения корней уравнения (20) необходимо сначала определить интервалы, на концах которых функция изменяет знак. Для этого можно воспользоваться функцией SignChange, а число таких интервалов определить при помощи NCount. Только в этом случае вместо параметра V_0 необходимо использовать нуль, а параметр V_max заменить на .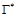

В результате массив SignChange будет содержать середины интервалов, на концах которых функция меняет знак. После этого остается на каждом из этих интервалов определить корни:

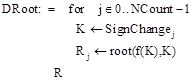
В результате в массив DRoot будут записаны все корни уравнения (20), например:

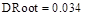
Из этого следует, что на выбранной частоте может распространяться только одна волна .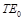

После этого необходимо численно решить уравнение (20) для другой частоты V.

Заметим, что при 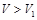( 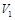— нормированная частота отсечки волны 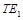или элемент массива 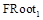) при решении уравнения (20) массив DRoot будет содержать уже два элемента, например:

Первый корень относится к волне 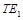, которая возникла только с частоты отсечки 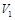; а второй корень — к волне 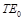. Большее значение корня всегда соответствует волне с меньшим вторым индексом.

Продолжая процесс численного решения уравнения (20) при различных значениях нормированной частоты 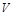мы получаем спектр дисперсионных кривый, соответствующих различным собственным волнам.

Вам необходимо рассчитать дисперсионные характеристики при значениях нормированной частоты 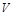в пределах от 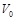до 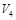с шагом 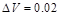. В результате необходимо построить дисперсионные кривые для первых четырех TE или TM-мод (см. вариант).

На рис.2 показан примерный вид дисперсионных характеристик.

По результатам расчетов дисперсионных характеристик определить частотный диапазон одноволновости, в котором возможно распространение только нулевой TE или TM-моды.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Виды оптических волноводов, используемых в интегральной оптике.

2. Уравнения Максвелла для описания электромагнитных полей волн в оптических волноводах.

3. TE и TM-моды.

4. Уравнения Гельмгольца для TE и TM-мод.

5. Вывод дисперсионного уравнения для TE-мод плоского трёхслойного оптического волновода.

6. Вывод дисперсионного уравнения для TM-мод плоского трёхслойного оптического волновода.

7. Алгоритм расчёта частот отсечек и дисперсионных характеристик собственных волн плоского трёхслойного оптического волновода.

8. Численный расчёт дисперсионных характеристик.

9. Матричная теория описания электромагнитных волн в многослойных оптических волноводах.

10. Применение матричной теории для вывода дисперсионного уравнения для TE-мод трёхслойного диэлектрического волновода.

ЛИТЕРАТУРА

1. Интегральная оптика / Под ред. Тамира Т. — М.: Мир, 1978.

2. Волноводная оптоэлектроника / Под ред. Тамира Т. — М.: Мир, 1991.

3. Унгер Х.-Г. Планарные и волоконные оптические волноводы. — М.: Мир, 1980.

Поиск по сайту: