АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Упражнение 1. Метод бисекции (метод деления пополам)

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Открытые способы определения поставщика.
  4. I. Предмет и метод теоретической экономики
  5. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  6. II. Метод упреждающего вписывания
  7. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  8. II. Методы непрямого остеосинтеза.
  9. II. Проблема источника и метода познания.
  10. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  11. III. Методологические основы истории
  12. III. Предмет, метод и функции философии.

Пусть задано уравнение вида , которое на некотором интервале 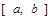имеет корень 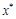, при котором .

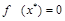Пусть график этой функции имеет вид, показанный на рисунке 1.

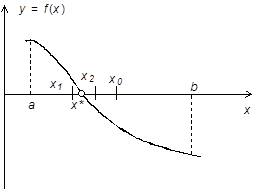
Рисунок 1


Если , это означает, что на интервале 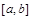имеется корень 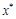. Метод бисекции заключается в следующем. Первое приближение выбирается в виде середины интервала :

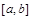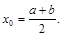
Если 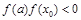, то корень лежит в интервале 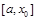, в противном случае в 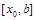. Для функции, показанной на рисунке 1 выполняется первое условие, поэтому второе приближение выбирается в виде середины интервала :

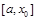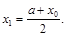
Если 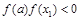, то корень лежит в интервале , в противном случае в 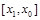. Для функции, показанной на рисунке 1 выполняется второе условие, поэтому третье приближение выбирается в виде середины интервала :

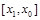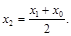
Подобный процесс выполняется до тех пор, пока где 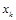— 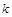-ое приближение к корню; 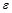— наперед заданное малое число.

Алгоритм метода бисекции в среде MathCad выглядит следующим образом:

При помощи функции Bisection (a,b, 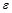) найдите корень заданной функции с точностью 10–6:

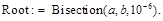
Концы интервала смены знака 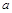и должны быть заданы в начале программы.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)