Упражнение 2. Метод хорд

Пусть задано уравнение вида , которое на некотором интервале 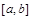имеет корень 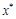, при котором .

Пусть график этой функции имеет вид, показанный на рисунке 2.

Рисунок 2

Если , это означает, что на интервале 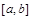имеется корень 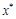. Метод хорд заключается в следующем. Проводим хорду из точки в точку и в качестве первого приближения выбираем точку :

Если 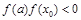, то корень лежит в интервале 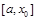, в противном случае в 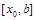. Для функции, показанной на рисунке 2 выполняется первое условие, поэтому проводим хорду из точки в точку и в качестве первого приближения выбираем точку :

Если 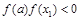, то корень лежит в интервале , в противном случае в 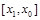. Для функции, показанной на рисунке 2 выполняется второе условие, поэтому проводим хорду из точки в точку и в качестве первого приближения выбираем точку :

Подобный процесс выполняется до тех пор, пока где 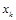— 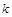-ое приближение к корню; 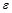— наперед заданное малое число.

Общая формула выбора приближения для метода хорд имеет вид:

Алгоритм метода хорд в среде MathCad выглядит следующим образом:

При помощи функции Chord (a,b, 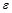) найдите корень заданной функции с точностью 10^–6:

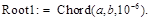
Концы интервала смены знака 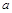и должны быть заданы в начале программы.

Измените функции Bisection (a,b, 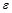) и Chord (a,b, 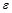) таким образом, чтобы они могли подсчитать число итераций необходимых для поиска корня с заданной точностью (для этого создайте целочисленный параметр 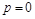в начале функций, который затем при каждой итерации увеличивается на единицу).

Сделайте вывод о том, какой из двух методов является более быстродействующим.

Поиск по сайту: