Упражнение 1. Расчет нормированных частот отсечек

1. В программе MathCad откройте новый документ и организуйте ввод параметров задачи: и (номер моды).

2. По формуле (2) вычислите параметр асимметрии 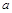. Сделайте вывод о том, симметричным или асимметричным является оптический волновод при заданных параметрах.

3. По формуле (8) определите частоты отсечек :

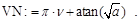
Изменяя номер моды рассчитайте значения нормированных частот отсечек первых трёх низших мод волновода:

Определите диапазон одноволновости: .

Упражнение 2. Расчет нормированных дисперсионных характеристик b = b (V).

1. Введите номер моды, для которой рассчитывается характеристика.

2. Введите число точек дисперсионной характеристики .

3. Введите шаг расчета дисперсионной характеристики: .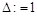

4. Вычислите массив значений нормированной частоты, для которых будет производиться расчет:

Внимание: для набора нижнего n нажмите кнопку [; для набора.. — нажмите кнопку а:а.

5. Введите дисперсионное уравнение (3):

6. Введите начальное приближение: .

7. Для каждого значения нормированной частоты рассчитайте значение нормированной постоянной распространения:

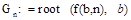
8. Составьте таблицу:

Частота V	Постоянная распространения b
...	...

9. Постройте график по данным таблицы.

10. Повторите расчет дисперсионных характеристик для мод (пп. 1-9). Зависимости для мод постройте в одной системе координат. Пример приведён на рисунке 2.

Рисунок 2

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Понятие дисперсионной характеристики моды в оптическом волноводе.

2. Типы мод оптических волноводов.

3. Характеристики мод в оптическом волноводе: частота отсечки, частота, длина волны, постоянная распространения, фазовая скорость, групповая скорость.

4. Запредельный и одноволновый режимы работы оптического волновода.

5. Нормированные характеристики мод в оптическом волноводе.

6. Метод расчёта дисперсионных характеристик мод.

7. Использование программного пакета MathCad для расчёта дисперсионных характеристик мод.

8. Принцип вычисления корней с помощью функции root.

ЛИТЕРАТУРА

1. Интегральная оптика / Под ред. Тамира Т. — М.: Мир, 1978.

2. Волноводная оптоэлектроника / Под ред. Тамира Т. — М.: Мир, 1991.

3. Унгер Х.-Г. Планарные и волоконные оптические волноводы. — М.: Мир, 1980.

ЛАБОРАТОРНАЯ РАБОТА №4

Исследование интегрального электрооптического
вращателя плоскости поляризации

ЦЕЛЬ РАБОТЫ: получение навыков расчёта характеристик интегральных электрооптических вращателей плоскости поляризации и выбора параметров изучаемых устройств.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1. Эффект Поккельса в кристаллах

Устройства для модуляции, разделения и контроля поляризации находят широкое применение в системах оптической связи когерентного типа. Примером такого устройства может служить интегральный оптический преобразователь излучения TE Û TM.

В основе работы поляризационных устройств лежит электрооптический эффект Поккельса в кристаллах. Известно, что для анизотропных сред (к которым относятся и кристаллы) одно из материальных уравнений принимает тензорный вид:

(1)

где

—

— тензор диэлектрической проницаемости.

В любом кристалле всегда существуют три взаимоперпендикулярных направления, такие что вдоль этих осей

(2)

Эти оси называются главными оптическими осями и относительно их тензор диэлектрической проницаемости приводится к диагональному виду. По аналогии можно ввести тензор показателей преломления:

(3)

где — магнитная проницаемость кристалла (в большинстве случаев её можно положить равной 1).

Из закона сохранения энергии можно получить для плотности электрической энергии следующее выражение:

(4)

Обозначая:

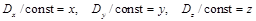
приходим к уравнению эллипсоида

(5)

Уравнение (5) описывает эллипсоид показателей преломления.

При приложении внешнего электрического поля (эффект Поккельса) произойдёт линейное изменение элементов тензора показателей преломления на величину

(6)

где — показатель преломления обыкновенной или необыкновенной волны в кристалле; — элементы электрооптического тензора размерности 3 x 6. Учитывая коэффициенты тензора можно найти шесть значений изменения показателя преломления в виде симметричной матрицы 6 x 3. Например, если в качестве материала для создания поляризационного устройства выступает ниобат лития, то для него данный тензор имеет вид:

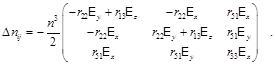(7)

Недиагональные элементы матрицы (7) определяют электрооптическое взаимодействие между ортогонально поляризованными компонентами электромагнитной волны. Например, коэффициент

(8)

задает вращение эллипсоида показателей преломления, которое благодаря наличию составляющей 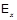внешнего электрического поля приводит к появлению связи между ортогональными составляющим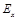и и поля электромагнитной волны.

Таким образом, недиагональные элементы матрицы электрооптических коэффициентов определяют изменение поляризации и появляется возможность создания интегрально-оптических поляризационных устройств (например, на основе волноводов типа ).

2. Поляризация электромагнитной волны

Электромагнитная волна характеризуется тремя векторами: (вектор напряженности электрического поля), (вектор напряженности магнитного поля) и (вектор Умова-Пойнтинга, задающий направление переноса волной энергии).

Поляризация — это направление колебаний вектора электро-магнитного поля (ЭМП) волны в пространстве при фиксированном направлении распространения. Плоскость поляризации — это плоскость, в которой лежат векторы и .

Существуют следующие виды поляризации:

— линейная, когда вектор совершает колебания вдоль выбранного направления (по прямой линии);

— круговая, когда вектор вращается по окружности (правокруговая — вращается против часовой стрелки; левокруговая — по часовой стрелке);

— эллиптическая, когда вектор вращается по эллипсу (правоэллиптическая — вращается против часовой стрелки; левоэллиптическая — по часовой стрелке);

— хаотическая, когда вектор в различных точках пространства колеблится в различных направлениях.

Различные виды поляризации электромагнитной волны (ЭМВ) показаны на рисунке 1.

Рисунок 1

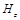В оптических волноводах распространяются электромагнитные волны с двумя типами линейной поляризацией. Рассмотрим их на примере распространения электромагнитной волны в канальном световоде (рисунок 2 а). В общем случае в структуре поля ЭМВ могут присутствовать шесть составляющих ЭМП: . Составляющие и называются продольными. В канальном волноводе возможно распространение мод с двумя ортогональными линейными поляризациями.

1. TE-волна (H-волна) (рисунок 2 б) — поперечно-электрическая волна, у которой в структуре поля отсутствует продольная составляющая электрического поля; она имеет следующие составляющие: .

1. TM-волна (E-волна) (рисунок 2 в) — поперечно-электрическая волна, у которой в структуре поля отсутствует продольная составляющая 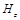магнитного поля; она имеет следующие составляющие: .

В электродинамике существует теорема, согласно которой ЭМВ с произвольной эллиптической поляризацией всегда можно представить в виде суперпозиции двух волн TE и TM с различными амплитудами.

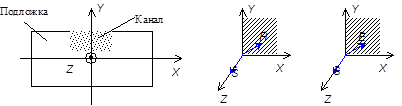
а) б) в)

Рисунок 2

Для характеристики поляризации волны удобно использовать два параметра: угол поляризации и фазовый сдвиг между TE и TM составляющими . Угол поляризации определяет отношение амплитуд TE и TM волн. В связи с этим комплексные амплитуды TE и TM волн представляются в виде:

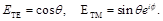(9)

Условием линейной поляризации излучения является равенство нулю фазового сдвига . В этом случае электромагнитная волна линейно поляризована под углом . Если , то в составе излучения присутствует только TE-составляющая; если 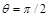— только TM-составляющая. Правокруговая поляризация описывается набором параметров Левокруговая поляризация — Для эллиптически-поляризованной волны углы и принимают произвольные значения.

Для ряда практических задач необходимо создание интегральных оптических устройств способных преобразовывать поляризацию входного излучения (i — «input» — вход) в определенную поляризацию (o — «output» — выход) на выходе:

Такое устройство для преобразования поляризации имеет очень большое значение, поскольку обыкновенное одномодовое оптическое волокно не сохраняет поляризации, в то время как когерентные системы связи требуют использование сигналов с известной поляризацией. Во многих случаях вполне достаточно, чтобы выходной сигнал представлял собой TE или TM-моду. При этом на вход устройства может поступать произвольный эллиптически-поляризованный сигнал.

3. Интегрально-оптический вращатель плоскости поляризации

Устройство интегрально-оптического вращателя плоскости поляризации приведено на рисунке 3 (вид на подложку сверху). ИОС изготавливается на подложке из (ниобат лития), волноводная система представляет собой канальный волновод на основе соединения . Принцип работы данного устройства основан на электрооптическом эффекте Поккельса. Основным элементом рассматриваемого устройства является периодическая металлическая электродная структура 2, выполняющая роль преобразователя типа поляризации. Данным элемент помещается между двумя фазосдвигающими ячейками 1 и 3, назначение которых состоит в изменении фазового сдвига между TE и TM-составляющими электромагнитного излучения в канальном волноводе.

Рисунок 3

Рассмотрим принцип работы электрооптического вращателя плоскости поляризации.

Первая фазосдвигающая ячейка характеризуется матрицей передачи вида

(10)

где — фазовый сдвиг, создаваемый ячейкой 1.

Матрица передачи электрооптического преобразователя поляризации имеет вид:

(11)

где — длина периодической электродной системы; — параметр, пропорциональный коэффициенту , управляющему напряжению и показателю преломления канального волновода .

Вторая фазосдвигающая ячейка описывается следующей матрицей передачи:

(12)

где 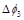— фазовый сдвиг, создаваемый ячейкой 3.

Матрица передачи всего устройства получается путем перемножения матриц передачи отдельных его участков (10), (11) и (12) и имеет вид:

(13)

Используя выражение (13), несложно получить соотношения для угла поляризации на выходе устройства

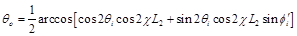(14)

и относительного наведённого фазового сдвига

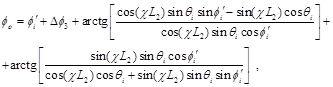(15)

где — относительный наведённый фазовый сдвиг после первого фазосдвигающего участка на входе участка преобразования типа поляризации излучения.

Процесс преобразования поляризации происходит в три этапа.

1. На вход устройства подается эллиптически-поляризованное излучение (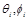). После прохождения волной первого фазосдвигающего участка под действием модулирующего напряжения 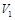между TE и TM-составляющими появляется дополнительный наведённый сдвиг фазы , а угол поляризации остаётся неизменным.

2. На участке 2 происходит преобразование типа поляризации световой волны, а именно изменяется угол поляризации . Это является следствием электрооптического эффекта Поккельса — появление недиагональных элементов тензора приводит к наличию связи между TE и TM-составляющими, что в свою очередь ведёт к изменению их амплитуд. В результате этого процесса плоскость поляризации поворачивается на некоторый угол, определяемый значениями .

3. На втором фазосдвигающем участке 3 вследствие действия модулирующего напряжения происходит дополнительный наведенный фазовый сдвиг 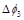, который необходим для получения нужного типа поляризации излучения на выходе.

Наличие первого фазосдвигающего участка необходимо для обеспечения возможности произвольного преобразования поляризации. На рисунке 4 приведены зависимости угла поляризации на выходе устройства 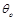от величины параметра связи 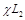при различных значениях угла поляризации на входе 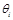. Зависимости построены в предположении отсутствия первого фазосдвигающего участка, то есть при 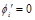. Из графиков видно, что если на входе сигнал представлен только TE или TM поляризацией ( или ), то на выходе устройства можно получить произвольное значение угла поляризации 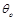за счет выбора соответствующего параметра связи .

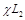Однако когда угол , то диапазон допустимых значений 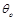ограничивается некоторым интервалом значений. Например, при : . Более того, из рисунка 4 несложно заметить, что для угла поляризации (круговая поляризация) вообще не удается произвести изменение типа поляризации ни при одном значении параметра связи 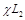. Кроме того, можно отметить, что и при диапазон допустимых значений 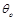будет ограничен.

Для обеспечения возможности произвольного преобразования угла поляризации необходимо, чтобы первый фазосдвигающий участок создавал относительное изменение фазы между TE и TM-составляющими . В этом случае из выражения (14) несложно получить, что

(16)

Рисунок 4

В этом случае происходит вращение плоскости поляризации по линейному закону и преобразователь работает в режиме линейного вращателя.

В результате можно сделать вывод, что лишь в двух частных случаях при возможно произвольное преобразование типа поляризации. Следовательно, наличие первого фазосдвигающего участка необходимо для того, чтобы сделать сдвиг фаз равным одному из двух значений.

Относительный сдвиг фазы на выходе устройства 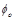определяется вторым фазосдвигающим участком 3 (рисунок 3). В оптимальном случае:

(17)

Из данного соотношения следует, что относительный фазовый сдвиг на выходе преобразователя мод такой же, как и на его входе.

Режим линейного вращателя плоскости поляризации реализуется, когда первый фазосдвигающий участок дает сдвиг , а второй — . При произвольной поляризации на входе и необходимости получения TE или TM-поляризации на выходе величина 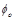не имеет значения и второй фазосдвигающий участок не нужен.

В случае, когда на вход устройства подается TE или TM-поляризованное излучение, наоборот, не нужен первый фазосдвигающий участок и в этом случае на выходе можно получить произвольный тип поляризации.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

Поиск по сайту: