 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос27 Полярная и декартова системы координат на плоскости. Связь между полярными и декартовым системами координат. Цилиндрические и сферические системы координат на плоскости
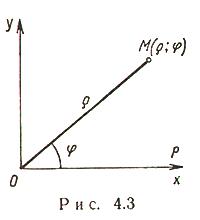
Полярные координаты (рис. 4.3)
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается  , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.[1]
, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.[1]
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
О - полюс, Ox - полярная ось,  - полярный радиус,
- полярный радиус,  - полярный угол.
- полярный угол.

 Главные значения
Главные значения  и
и  : (иногда
: (иногда
Выражение декартовых прямоугольных координат через полярные


Выражение полярных координат через декартовы прямоугольные

Цилиндрические координаты (рис. 4.6)

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой z), которая задаёт высоту точки над плоскостью.
Точка P даётся как  . В терминах прямоугольной системы координат:
. В терминах прямоугольной системы координат:
 — расстояние от O до P ', ортогональной проекции точки P на плоскость XY. Или то же самое, что расстояние от P до оси Z.
— расстояние от O до P ', ортогональной проекции точки P на плоскость XY. Или то же самое, что расстояние от P до оси Z.
 — угол между осью X и отрезком OP '.
— угол между осью X и отрезком OP '.
z равна аппликате точки P.
Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось Z взять в качестве оси симметрии. Например, бесконечно длинный круглый цилиндр в прямоугольных координатах имеет уравнение x 2 + y 2 = c 2, а в цилиндрических — очень простое уравнение ρ = c. Отсюда и идёт для данной системы координат имя «цилиндрическая».
Главные значения  ,
,  ,
,  :
: 
Связь между декартовыми прямоугольными и цилиндрическими координатами:

Сферические координаты (рис. 4.7)

Сферическую систему координат удобно определять, соотносясь с декартовой прямоугольной системой координат (см. рисунок):
Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат  , где r — расстояние до начала координат, а θ и
, где r — расстояние до начала координат, а θ и  — зенитный и азимутальный угол соответственно.
— зенитный и азимутальный угол соответственно.
Три координаты  определены как:
определены как:
 — расстояние от начала координат до заданной точки P.
— расстояние от начала координат до заданной точки P.
 — угол между осью Z и отрезком, соединяющим начало координат и точку P.
— угол между осью Z и отрезком, соединяющим начало координат и точку P.
 — угол между осью X и проекцией отрезка, соединяющего начало координат с точкой P, на плоскость XY (в Америке углы θ и
— угол между осью X и проекцией отрезка, соединяющего начало координат с точкой P, на плоскость XY (в Америке углы θ и  меняются ролями).
меняются ролями).
Угол θ называется зенитным, или полярным, или нормальным, а также он может быть назван английским словом colatitude, а угол  — азимутальным. Углы θ и
— азимутальным. Углы θ и  не имеют значения при r = 0, а
не имеют значения при r = 0, а  не имеет значения при sin(θ) = 0 (то есть при θ = 0 или
не имеет значения при sin(θ) = 0 (то есть при θ = 0 или  ).
).
Главные значения  ,
,  ,
,  :
: 
Иногда вместо 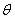 рассматривают
рассматривают 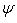 :
: 
Связь между декартовыми прямоугольными и сферическими координатами
 или
или 
Вопрос28 Множество. Способы задания и примеры числовых множеств. Точные верхняя и нижняя граница множеств. Счетные и несчетные множества. Подмножество. Объединение, пересечение и разность двух множеств. Декартово произведение множеств.
Множества
как такового, определения множества не существует в природе (о как нахJ!) но тем не менее, некоторые учены считают так:
Георг Кантор:
Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).
Бертран Расселл: «Множество суть совокупность различных элементов, мыслимая как единое целое».
Множество A, состоящее из элементов x, y,...:


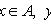

Множество A, состоящее из элементов x, удовлетворяющих условию P:
A = { x | x удовлетворяет условию P }.

 - пустое множество.
- пустое множество.

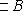 - A является подмножеством B.
- A является подмножеством B.

 - A не является подмножеством B.
- A не является подмножеством B.
A = B - множества A и B совпадают,




Два множества A и B могут вступать друг с другом в различные отношения.
A включено в B, если каждый элемент множества A принадлежит также и множеству B:

A включает B, если B включено в A:

A равно B, если A и B включены друг в друга:

A строго включено в B, если A включено в B, но не равно ему:

A строго включает B, если B строго включено в A:

A и B не пересекаются, если у них нет общих элементов:
 и
и  не пересекаются
не пересекаются 
A и B находятся в общем положении, если существует элемент, принадлежащий исключительно множеству A, элемент, принадлежащий исключительно множеству B, а также элемент, принадлежащий обоим множествам:
 и
и  находятся в общем положении
находятся в общем положении 

Подмно́жество в теории множеств — это понятие части множества.
 Определения
Определения
Множество A является подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B. Пишут:  или
или  . Таким образом,
. Таким образом,

Множество B в таком случае называется надмно́жеством множества A, и этот факт часто записывают:  или
или 
Множество A называется подмножеством множества B, если все элементы A являются также элементами B. Любое множество является своим подмножеством:  Если при этом
Если при этом  , то A называется собственным подмножеством B. По определению полагают, что пустое множество является подмножеством любого множества:
, то A называется собственным подмножеством B. По определению полагают, что пустое множество является подмножеством любого множества:  .
.
Множество всех подмножеств множества A обозначается  или 2 A, так как оно соответствует множеству отображений из A в 2 = {0,1}. Иногда его называют множеством-степенью (англ. power set) для A. Мощность множества-степени, по теореме Кантора, всегда больше, чем у исходного множества. В категории множеств
или 2 A, так как оно соответствует множеству отображений из A в 2 = {0,1}. Иногда его называют множеством-степенью (англ. power set) для A. Мощность множества-степени, по теореме Кантора, всегда больше, чем у исходного множества. В категории множеств  — это контравариантный функтор, отображающий функцию
— это контравариантный функтор, отображающий функцию  в
в  при этом отображение
при этом отображение  ставит в соответствие каждому подмножеству B его полный прообраз в A.
ставит в соответствие каждому подмножеству B его полный прообраз в A.
Примеры:
Подмножествами множества {0,1,2,3,4,5} являются множества 
Подмножествами множества  являются множества
являются множества 
Пусть A = { a, b }, тогда 
Собственное подмножество
Из определения прямо следует, что пустое множество обязано быть подмножеством любого множества. Также, очевидно, любое множество является своим подмножеством:
 .
.
Если  , и
, и  ,
,  , то A называется со́бственным или нетривиа́льным подмножеством.
, то A называется со́бственным или нетривиа́льным подмножеством.
Свойства
Отношение подмножества обладает целым рядом свойств.[1]
Отношение подмножества рефлексивно:

Отношение подмножества антисимметрично:

Отношение подмножества транзитивно:

Пустое множество является подмножеством любого другого:

Таким образом отношение подмножества является отношением частичного порядка на булеане 2 M — семействе всех подмножеств любого объемлющего множества M.
Для любых двух множеств A и B следующие утверждения эквивалентны:




Подмножества конечных множеств
Если исходное множество конечно, то у него существует конечное количество подмножеств. А именно, у n -элементного множества существует 2 n подмножеств (включая пустое). Чтобы убедиться в этом, достаточно заметить, что каждый элемент может либо входить, либо не входить в подмножество, а, значит, общее количество подмножеств будет n -кратным произведением двоек. Если же рассматривать только подмножества n -элементного множества из  элементов, то их количество выражается биномиальным коэффициентом
элементов, то их количество выражается биномиальным коэффициентом  . Для проверки этого факта можно выбирать элементы подмножества последовательно. Первый элемент можно выбрать n способами, второй n − 1 способом, и так далее, и, наконец, k -й элемент можно выбрать n − k + 1 способом. Таким образом мы получим последовательность из k элементов, и ровно k! таким последовательностям соответствует одно подмножество. Значит, всего найдется
. Для проверки этого факта можно выбирать элементы подмножества последовательно. Первый элемент можно выбрать n способами, второй n − 1 способом, и так далее, и, наконец, k -й элемент можно выбрать n − k + 1 способом. Таким образом мы получим последовательность из k элементов, и ровно k! таким последовательностям соответствует одно подмножество. Значит, всего найдется  таких подмножеств.
таких подмножеств.
Пример
Пусть

Тогда
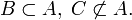
Объединение множеств







 (коммутативность),
(коммутативность),


 (идемпотентность),
(идемпотентность),


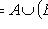
 (ассоциативность),
(ассоциативность),


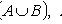


Пересечение множеств




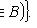


 (коммутативность),
(коммутативность),


 (идемпотентность),
(идемпотентность),
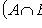
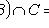

 (ассоциативность),
(ассоциативность),



 (дистрибутивность),
(дистрибутивность),





Разность множеств







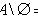


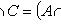
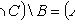







Декартово (прямое) произведение множеств



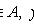






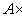

 - декартов квадрат множества A,
- декартов квадрат множества A,




Вопрос29 Высказывание. Значение истинности высказывания. Отрицание. Коъюнкция. Дизъюнкция. Импликация. Эквиваленция высказываний. Логическая формула, таблица истинности для формулы. Свойства операций над высказываниями.
Высказывание - повествовательное предложение, о котором можно говорить истинно оно или ложно.
Отрица́ние в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком перед или чертой над суждением. Синоним: логическое "НЕ".
Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".
Дизъю́нкция — (лат. disjunctio - разобщение) логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».
Импликация — бинарная логическая связка, по своему применению приближенная к союзам «если … то …».
Импликация записывается как посылка  следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие).
следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие).
Суждение, выражаемое импликацией, выражается также следующими способами:
Посылка является условием, достаточным для выполнения следствия;
Следствие является условием, необходимым для истинности посылки.
Эквивале́нция (или эквивале́нтность[1]) — двуместная логическая операция. Обычно обозначается символом ≡ или ↔. Задаётся следующей таблицей истинности:
| p |  
|
| 0 1 | 1 0 |
| p q |  
|  
| 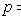 
|  
|
| 0 0 0 1 1 0 1 1 | 0 1 1 1 | 0 0 0 1 | 1 1 0 1 | 1 0 0 1 |
Основные равносильности
Закон двойного отрицания
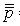

Идемпотентность




Коммутативность
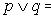



Ассоциативность


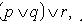


Дистрибутивность










Законы де Моргана




\
Вопрос30. Предикат. Множество истинности предиката. Кванторы общности существования. Виды формулировок теорем (прямая и обратная теоремы, теорема о необходимых и достаточных условиях).
Предика́т (лат. praedicatum — заявленное, упомянутое, сказанное) — любое математическое высказывание, в котором есть, по меньшей мере, одна переменная. Предикат является основным объектом изучения логики первого порядка.
Предикат – выражение с логическими переменными, имеющие смысл при любых допустимых значениях этих пременных.
Выражения: х > 5, x > y – предикаты.
Предика́т (n -местный, или n -арный) — это функция с множеством значений {0,1} (или «ложь» и «истина»), определённая на множестве  . Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».
. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».
Предикат можно связать с математическим отношением: если n -ка принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.
Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.
Предикат называют тождественно-истинным и пишут:

если на любом наборе аргументов он принимает значение 1.
Предикат называют тождественно-ложным и пишут:

если на любом наборе аргументов он принимает значение 0.
Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.
Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. д
Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают:
Квантор всеобщности (обозначение:  , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).
, читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).
Квантор существования (обозначение: 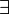 , читается: «существует…» или «найдётся…»).
, читается: «существует…» или «найдётся…»).
Поиск по сайту: