 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Графический способ
Числовые функции можно также задавать с помощью графика. Пусть 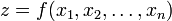 - вещественная функция n переменных.
- вещественная функция n переменных.
Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис ( ). Каждой точке функции сопоставим вектор:
). Каждой точке функции сопоставим вектор: 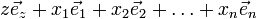 . Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим "школьное" определение графика функции.
Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств.
Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвертой координаты точки сопоставить некоторый цвет на графике)
Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x,
где k - постоянная величина (коэффициент пропорциональности).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол 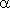 , тангенс которого равен k: tan
, тангенс которого равен k: tan 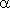 = k (рис.8). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = 3.
= k (рис.8). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = 3.
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x,
где k - постоянная величина.
 График обратной пропорциональности – гипербола (рис.10). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью (о конических сечениях см. раздел «Конус» в главе «Стереометрия»). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
График обратной пропорциональности – гипербола (рис.10). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью (о конических сечениях см. раздел «Конус» в главе «Стереометрия»). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
Основные характеристики и свойства гиперболы:
- область определения функции: x  0, область значений: y
0, область значений: y  0;
0;
- функция монотонная (убывающая) при x < 0и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0);
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a  0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.

Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a  0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
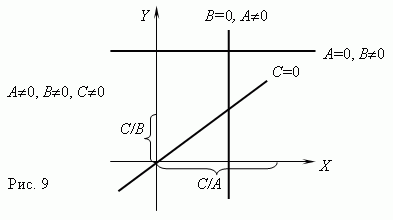
График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в начале координат, а в точке с координатами:
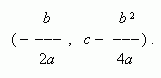
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x 2 и дискриминанта D: D = b 2 – 4 ac. Эти свойства следуют из анализа корней квадратного уравнения (см. соответствующий раздел в главе «Алгебра»). Все возможные различные случаи для квадратной параболы показаны на рис.12.
 Основные характеристики и свойства квадратной параболы:
Основные характеристики и свойства квадратной параболы:
- область определения функции:  < x +
< x +  (т.e. x
(т.e. x 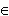 R), а область
R), а область
значений: … (ответьте, пожалуйста, на этот вопрос сами!);
- функция в целом не монотонна, но справа или слева от вершины
ведёт себя, как монотонная;
- функция неограниченная, всюду непрерывная, чётная при b = c = 0,
и непериодическая;
- при D < 0 не имеет нулей.
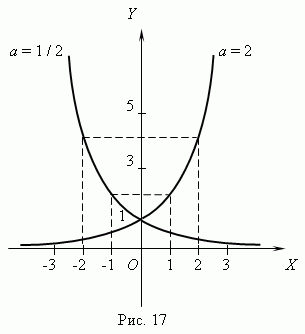 Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает. Основные характеристики и свойства показательной функции:
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает. Основные характеристики и свойства показательной функции:
- область определения функции: 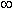 < x +
< x + 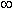 (т.e. x
(т.e. x 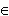 R);
R);
область значений: y > 0;
- функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- нулей функция не имеет.
 Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график (рис.18) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график (рис.18) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции:
- область определения функции: x > 0,а область значений: 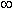 < y +
< y + 
(т.e. y  R);
R);
- это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- у функции есть один ноль: x = 1.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется графиком (рис.19). Эта кривая называется синусоидой.
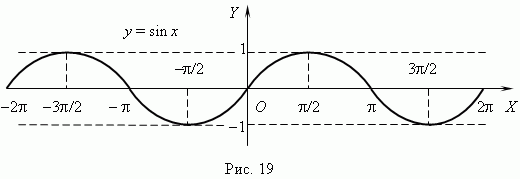
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на  2
2
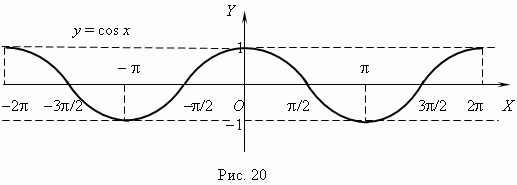
Из этих графиков очевидны характеристики и свойства этих функций:
- область определения:  < x +
< x +  область значений: 1
область значений: 1  y
y  +1;
+1;
- эти функции периодические: их период 2  ;
;
- функции ограниченные (| y |  , всюду непрерывные, не монотонные, но
, всюду непрерывные, не монотонные, но
имеющие так называемые интервалы монотонности, внутри которых они
ведут себя, как монотонные функции (см. графики рис.19 и рис.20);
- функции имеют бесчисленное множество нулей (подробнее см. раздел
«Тригонометрические уравнения»).
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
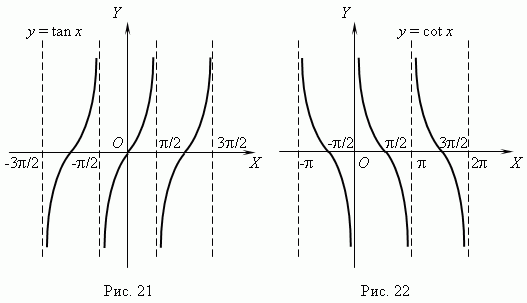
Из графиков видно, что эти функции: периодические (их период  ,
,
неограниченные, в целом не монотонные, но имеют интервалы монотонности
(какие?), разрывные (какие точки разрыва имеют эти функции?). Область
определения и область значений этих функций:
| 9. | Обратные тригонометрические функции. Определения обратных
тригонометрических функцийи их основные свойства приведены в
одноимённом разделе в главе «Тригонометрия». Поэтому здесь мы ограничимся
лишь короткими комметариями, касающимися их графиков, полученных
поворотом графиков тригонометрических функций вокруг биссектрисы 1-го
координатного угла.
|
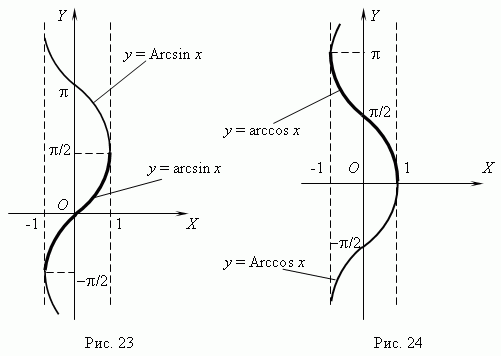
Функции y = Arcsin x (рис.23) и y = Arccos x (рис.24)многозначные, неограниченные; их область определения и область значений соответственно: 1  x
x  +1 и
+1 и  < y +
< y +  . Поскольку эти функции многозначные, не
. Поскольку эти функции многозначные, не
рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: 1  x
x  +1;
+1;
их области значений:  /2
/2  y
y 
 /2 для y = arcsin x и 0
/2 для y = arcsin x и 0  y
y 
 для y = arccos x;
для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
(y = arcsin x – возрастающая функция; y = arccos x – убывающая);
- каждая функция имеет по одному нулю (x = 0 у функции y = arcsin x и
x = 1 у функции y = arccos x).

Функции y = Arctan x (рис.25) и y = Arccot x (рис.26)- многозначные, неограниченные функции; их область определения: 
 x
x  +
+ 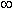 . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
. Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: 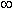
 x
x  +
+ 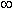 ;
;
их области значений:  /2< y <
/2< y <  /2 для y = arctan x и 0 < y <
/2 для y = arctan x и 0 < y <  для y = arccos x;
для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
(y = arctan x – возрастающая функция; y = arccot x – убывающая);
- только функция y = arctan x имеет единственный ноль (x = 0);
функция y = arccot x нулей не имеет.
Композиция функций
Если даны два отображения 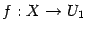 и
и 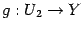 , где
, где  , то имеет смысл "сквозное отображение"
, то имеет смысл "сквозное отображение" 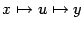 из
из  в
в 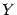 , заданное формулой
, заданное формулой 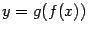 ,
, 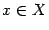 , которое называется композицией функций
, которое называется композицией функций 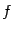 и
и  и обозначается
и обозначается  .
.

Рис.1.30.Сквозное отображение 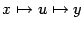 из
из  в
в 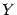
Таким образом, 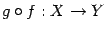 ,
, 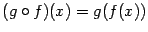 при всех
при всех 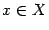 . Другое название композиции -- сложная функция (так как сквозное отображение
. Другое название композиции -- сложная функция (так как сквозное отображение 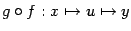 "сложено" из отображений
"сложено" из отображений 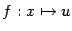 и
и 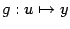 ).
).
Пример 1.18 Пусть  ,
, 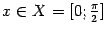 , и
, и 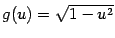 ,
, 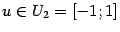 . Тогда
. Тогда 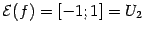 , и определена композиция
, и определена композиция
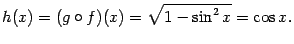
Упражнение 1.3 Покажите, что если заменить множество  в предыдущем примере на
в предыдущем примере на 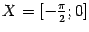 , то композиция
, то композиция  снова будет определена, но равна теперь
снова будет определена, но равна теперь 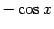 , а не
, а не 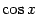 .
.
Пример 1.19 Пусть  ,
, 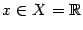 , и
, и  ,
, 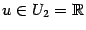 . Тогда определена композиция
. Тогда определена композиция  , заданная формулой
, заданная формулой 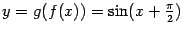 . По известной формуле приведения полученная композиция -- это косинус:
. По известной формуле приведения полученная композиция -- это косинус: 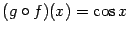 при всех
при всех 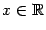 .
.
Замечание 1.5 Даже если для функций 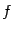 и
и  имеют смысл обе композиции
имеют смысл обе композиции 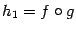 и
и 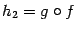 (что бывает далеко не для любой пары функций
(что бывает далеко не для любой пары функций 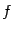 и
и  ), то функции
), то функции 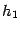 и
и  не обязаны совпадать; как правило, это не так.
не обязаны совпадать; как правило, это не так.
Пример 1.20 Пусть 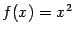 и
и 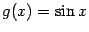 ,
,  . Тогда
. Тогда 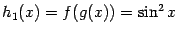 , а
, а  . Очевидно, что это разные функции:
. Очевидно, что это разные функции: 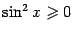 при всех
при всех 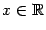 , а
, а 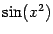 принимает значение
принимает значение  , например, при
, например, при 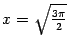 .
.
Применяя композицию функций, которые сами могут получаться как композиции, мы можем получать сложные функции вида  и более длинные композиции.
и более длинные композиции.
Вопрос33 Взаимно-однозначное соответствие между множествами. Обратное правило и обратная функция. Графики взаимно обратных функций. Определения, свойства и графики гиперболических функций. (тут уже начинается вынос мозга)
Мощностью конечного множества (множества, содержащего конечное число элементов) называется количество его элементов. Мощность множества A обозначается m (A).
Пример 1
Определите мощность множества A = {1, 3, 5, 7, 9} нечётных чисел.
Показать решение
Простым пересчётом элементов убеждаемся, что нечётных чисел всего 5, и потому m (A) = 5.
Ответ. 5.
Ясно (да ну!), что понятие мощности конечных множеств позволяет сравнивать их по количеству элементов. Так, если A = {1, 3, 5, 7, 9}, а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) > m (B).
Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Но иногда можно, как говорят, установить взаимно однозначное соответствие между двумя бесконечными множествами.
Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если из элементов этих множеств можно составить пары (a, b), причем каждый элемент из A и каждый элемент из B входят в одну и только одну пару.
Множества, между которыми установлено взаимно однозначное соответствие, содержат одинаковое количество элементов.
Множества A и B называют равномощными, если между их элементами можно установить взаимно однозначное соответствие (ещё говорят: можно установить взаимно однозначное отображение множеств).
Мощность множества натуральных чисел обозначается א. Алеф א – первая буква еврейского алфавита, так обозначается наименьшая возможная для бесконечных множеств мощность.
Множества, равномощные множеству натуральных чисел, называются счётными множествами.
Пример 2
Множество натуральных чисел равномощно множеству нечётных чисел, так как между ними можно установить взаимно однозначное соответствие, например, по следующему правилу:
1 2 3... n... ↕ ↕ ↕ ↕ 1 3 5... 2 n – 1...
Так как множество нечётных чисел является подмножеством натуральных чисел, то этот пример показывает, что бесконечное множество может быть равномощно своему подмножеству.
Пример 3
Множество положительных рациональных чисел счётно. Действительно, если представить каждое рациональное число в виде несократимой дроби и записать его в следующую таблицу, а затем пронумеровать, как указано на рисунке, то окажется, что множество рациональных положительных чисел действительно счётно.
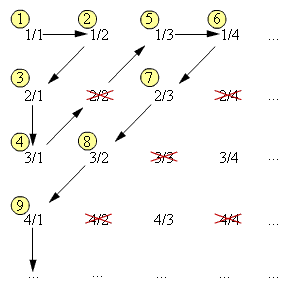 1
1
Рисунок 4.1.2.1.
Пример 4
Любой отрезок [ a; b ] равномощен отрезку [0; 1]. Взаимно однозначное соответствие между ними устанавливает формула y = (b − a) · x + a, где x 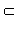 [0; 1], y
[0; 1], y 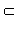 [ a; b ].
[ a; b ].
Пример 5
Множества  и
и  счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:
счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:
A 

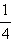 ...
... 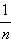 ... ↕ ↕ ↕ ↕ ↕ ↕ ↕ N 1 2 3... n... ↕ ↕ ↕ ↕ ↕ ↕ ↕ B 0
... ↕ ↕ ↕ ↕ ↕ ↕ ↕ N 1 2 3... n... ↕ ↕ ↕ ↕ ↕ ↕ ↕ B 0 
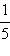 ...
...  ...
...
Существуют и другие бесконечные множества, мощность которых больше, чем мощность счётных множеств. Так, множество всех точек отрезка [0; 1] не равномощно множеству натуральных чисел  доказательство этой теоремы принадлежит немецкому математику Георгу Кантору.
доказательство этой теоремы принадлежит немецкому математику Георгу Кантору.
Как было показано в примере 4, множество всех точек отрезка [0; 1] равномощно множеству точек отрезка любой длины. Легко показать равномощность множеств отрезка [ a; b ] и интервала (a; b), а также отрезка [ a; b ] и луча (a; +∞). Наконец, можно доказать равномощность множеств всех точек отрезка и квадрата.
Мощность множества всех действительных чисел (или, что то же, множества всех точек числовой оси) обозначается символом c («континуум»). Поскольку множество всех действительных чисел несчётно, то א < c.
Континуум – не самая большая из бесконечных мощностей. Так, мощность множества всех подмножеств точек числовой оси больше, чем мощность самого множества всех точек оси. Она обозначается 2 c и называется гиперконтинуумом.
Обратная функция. Теорема о существовании и непрерывности обратной функции.
Понятие обратной функции.
Пусть функция y=f(x), заданная на множестве X, обратима. Это значит, что функция f различным значениям аргумента ставит в соответствие различные значения функции, т.е. для любых x1,x2∈X: x1/=x2⇒f(x1)/=f(x2).
В этом случае для каждого y∈Y=f(X) существует один и только один элемент x∈X такой, что y=f(x). А это означает, что на множестве Y определена функция g:Y→X, которую и называют обратной функцией к функции y=f(x) и обозначают: x=f−1(y). При этом очевидно, что функция f является обратной к функции f−1. Поэтому функции y=f(x) и x=f−1(y) называют взаимно обратными. Т.о., если функция f:X→Y, где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любом x∈X, f−1(f(y))=y при любом
y∈Y.
График. Переход от функции y=f(x), x∈X, к обратной функции x=f−1(y), y∈Y (если она существует), сводится лишь к измерению ролей множеств X и Y. Поэтому графики функций y=f(x) и x=f−1(y) на плоскости XOY совпадают. Но обычно и для обратной функции аргумент обозначают через y, т.е. записывают ее в видеy=f−1(x), x∈Y. Тогда график функции y=f−1(x) получается из графика прямой функции y=f(x) с помощью преобразования плоскости XOY, переводящей каждую точку (x,y) в точку (y,x), т.е. симметрией относительно прямой y=x.
Обычно, говоря об обратной функции, заменяют x на y, а y на x (x↔y) и пишут y=f−1(x). Очевидно, что исходная функция f(x)и обратная функция f−1(x) удовлетворяют соотношению:
f−1(f(x))=f(f−1(x))=x.
Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.
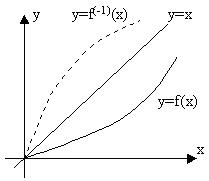
Монотонные функции и их свойства.
Пусть функция f(x)определена в некоторой области X. Функция называется возрастающей (убывающей) в этой области, если для любой пары принадлежащих ей значений x1и x2 из x1>x2 следуетf(x1)>f(x2) (f(x1)<f(x2)). Если же из x1>x2 следует f(x1)≥f(x2) (f(x1)≤f(x2)), то функцию называют неубывающей (невозрастающей). Иногда удобнее и в этом случае называть функцию возрастающей (убывающей) - но в широком смысле.
Функции всех этих типов носят общее название монотонных.
Существование и непрерывность обратной функции.
Теорема 1. Если функция y=f(x) строго возрастает (убывает) на множестве X, то для нее существует обратная функция x=f−1(y), которая определена на множестве Y=f(X) и является на Y строго возрастающей (убывающей).
Доказательство. По условию функция f строго возрастает на множестве X. Это значит для любых x1,x2∈X и x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X. Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2. По условию функция f строго возрастает на X, поэтому из условия x1≥x2 вытекает неравенствоy1=f(x1)≥y2=f(x2), что противоречит условию y1<y2.
Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.
Теорема 2. Если функция y=f(x) строго возрастает (убывает) и непрерывна на промежутке I, то существует обратная функция x=f−1(y), которая определена на промежутке Ef=f(I) и является на Е, строго возрастающей (убывающей) и непрерывной.
Доказательство. Для определенности предположим, что функция f строго возрастает на промежутке I. По следствию из 2-ой теоремы Больцано-Коши область значений Ef=f(I) непрерывной функции f тоже есть промежуток. В силу строгого возрастания функции f для каждого y∈E существует единственная точка x∈I такая, что f(x)=y. Следовательно для функции f существует обратная функция f−1 определенная на промежутке Е и с множеством значений I.
Покажем, что f−1 строго возрастает на Е. Пусть y1 и y2-- две произвольные точки из Е, такие, что y1<y2 и прообразами этих точек будут точки x1и x2. f−1(y1)=x1, и f−1(y2)=x2.
Поскольку f - строго возрастающая функция, то неравенство y1=f(x1)<f(x2)=y2 возможно тогда и только тогда когда x1<x2 или тоже самое, когда f−1(y1)<f−1(y2). В силу произвольности y1 и y2 ∈E делаем вывод, что функция f−1 - строго возрастает на множестве Е. Что и требовалось доказать.
1. Гиперболическими синусом, косинусом, тангенсом и котангенсом называются функции:
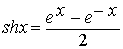 ;
; 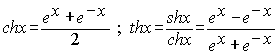 ;
;  .
.
Областью определения функций shx, chx, thx является вся числовая ось; функция y=cthx не определена в точке х=0. Название гиперболических функций (синус, косинус, …) объясняется тем, что для них справедливы тождества ''похожие'' на тригонометрические:
ch(x± y)=chx · chy ± shx · shy, (1)
sh(x± y)=shx · chy± chx · shy, (2)
ch2x–sh2x=1, (3)
ch2x=ch2x+sh2x, (4)
sh2x=2shx · chx. (5)
Тождества (2) и (5) аналогичны соответствующим формулам тригонометрии, а формулы (1), (3) и (4) отличаются от тригонометрических только знаком. Доказываются тождества (1) – (5) непосредственной проверкой. Более подробно о тождествах для гиперболических функций изложено в разделе III.
2. Рассмотрим уравнение гиперболы:

Его можно записать в параметрическом виде, используя гиперболические функции (этим и объясняется их название).
Обозначим y= b·sht, тогда х2 / а2=1+sh2t =ch2t. Откуда x=± a·cht.
Таким образом мы приходим к следующим параметрическим уравнениям гиперболы:
x= ± a ·cht,
у= в ·sht, –  < t <
< t <  . (6)
. (6)
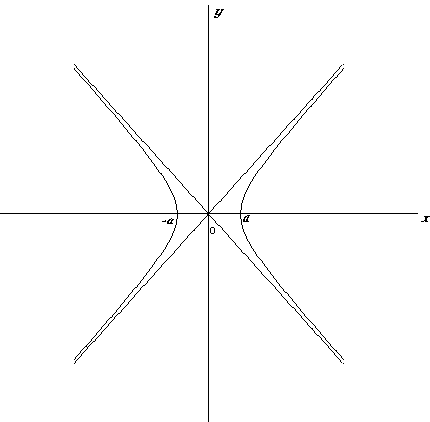
Рис. 1.
Знак ''+'' в верхней формуле (6) соответствует правой ветви гиперболы, а знак ''– '' - левой (см. рис. 1). Вершинам гиперболы А(– а; 0) и В(а; 0) соответствует значение параметра t=0.
Для сравнения можно привести параметрические уравнения эллипса, использующие тригонометрические функции:
x=а·cost,
y=в·sint, 0  t
t  2p. (7)
2p. (7)
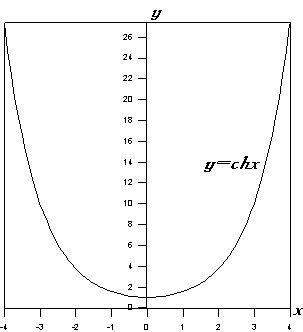
3. Очевидно, что функция y=chx является четной и принимает только положительные значения. Функция y=shx – нечетная, т.к.:
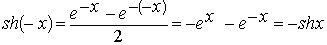 .
.
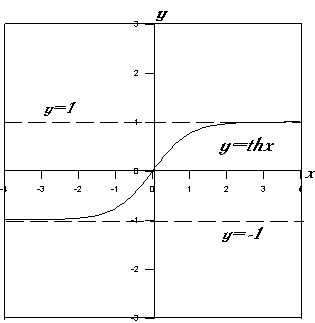
Функции y=thx и y=cthx являются нечетными как частные четной и нечетной функции. Отметим, что в отличие от тригонометрических, гиперболические функции не являются периодическими.
4. Исследуем поведение функции y= cthx в окрестности точки разрыва х=0:
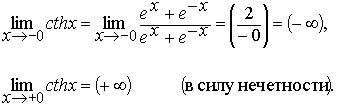
Таким образом ось Оу является вертикальной асимптотой графика функции y=cthx. Определим наклонные (горизонтальные) асимптоты:
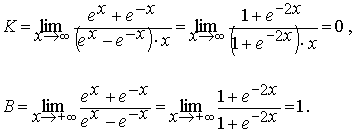
Следовательно, прямая у=1 является правой горизонтальной асимптотой графика функции y=cthx. В силу нечетности данной функции ее левой горизонтальной асимптотой является прямая у= –1. Нетрудно показать, что эти прямые одновременно являются асимптотами и для функции y=thx. Функции shx и chx асимптот не имеют.
5. Найдем производные основных гиперболических функций:
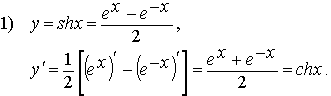
2) (chx)'=shx (показывается аналогично).

4) 
Здесь так же прослеживается определенная аналогия с тригонометрическими функциями. Полная таблица производных всех гиперболических функций приведена в разделе IV.
6. Нетрудно вычислить вторые производные основных гиперболических функций:
1) 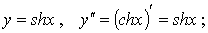
2) 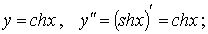
3) 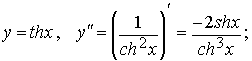
4) 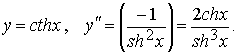
7. Используя результаты п. 1-6, строим графики основных гиперболических функций:

| 
|
| Рис. 2 | Рис. 3 |
| 
|
| Рис. 4 | Рис. 5 |
Вопрос34. Числовая последовательность. Предел числовой последовательности (конечный и бесконечный). Геометрическая иллюстрация. Теорема о сходимости монотонной и ограниченной последовательности.
Последовательность — это пздц (набор) элементов некоторого множества:
для каждого натурального числа можно указать элемент данного множества;
это число является номером элемента и обозначает позицию данного элемента в последовательности;
для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность.
В математике рассматривается множество различных последовательностей:
числовые последовательности;
временные ряды как числовой, так и не числовой природы;
последовательности элементов метрического пространства
последовательности элементов функционального пространства
последовательности состояний систем управления и автоматов.
Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей.
Определение
Пусть задано некоторое множество X элементов произвольной природы.
Всякое отображение 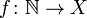 из множества натуральных чисел
из множества натуральных чисел 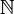 в заданное множество X называется последовательностью (элементов множества X).
в заданное множество X называется последовательностью (элементов множества X).
Образ натурального числа n, а именно, элемент xn = f (n), называется n -ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.
Связанные определения
Подмножество 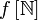 множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
множества X, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,
предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.
Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.
Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений. [1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.
Поиск по сайту: