Правило Крамера

Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель , элементами которого являются коэффициенты при неизвестных:

.

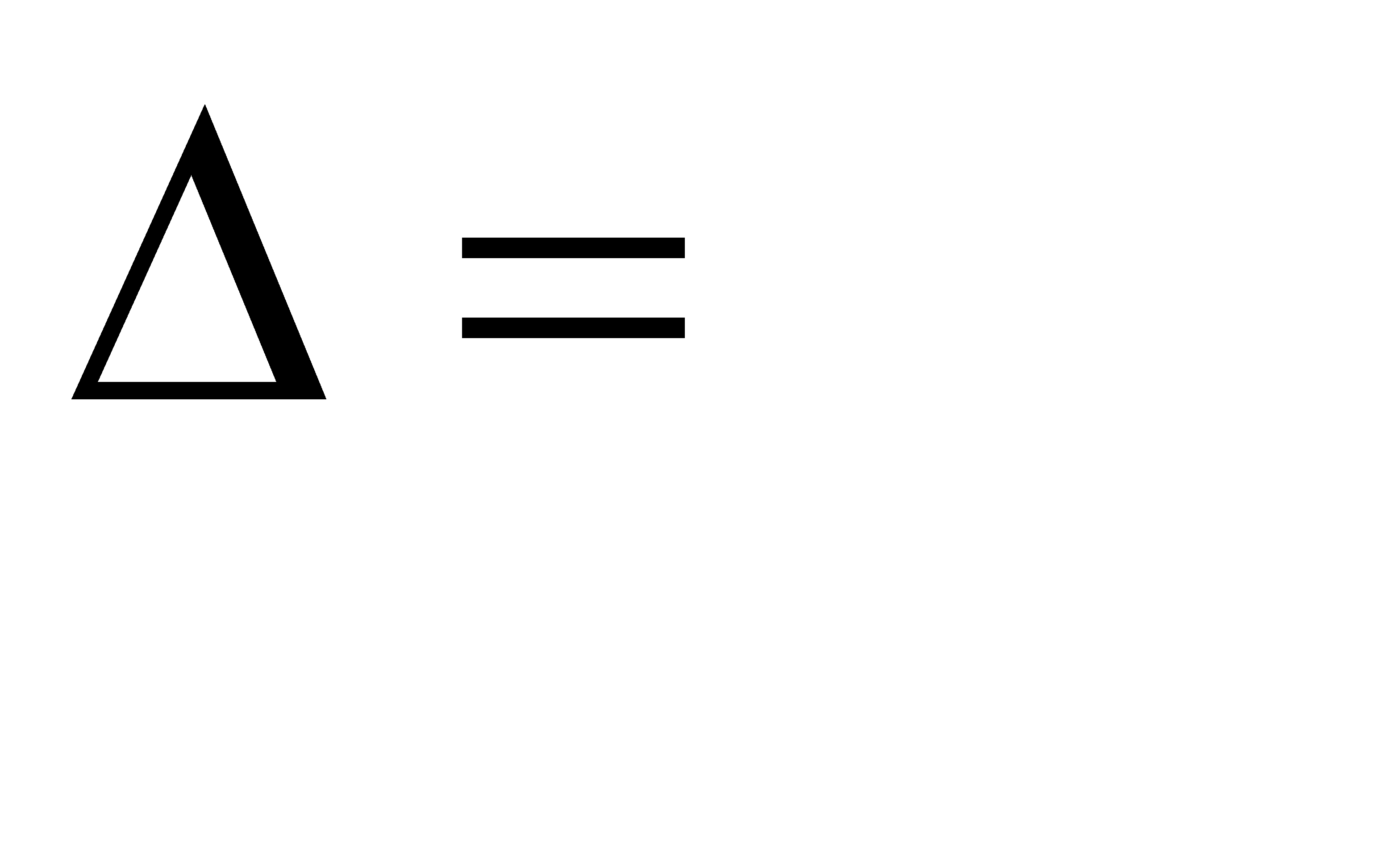
Предположим сначала, что Умножим каждое уравнение системы (2.3) на алгебраические дополнения элементов j-го столбца

Сложив затем все уравнения, получим:

. (2.5)

Отметим, что .

(j-й столбец)

(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при 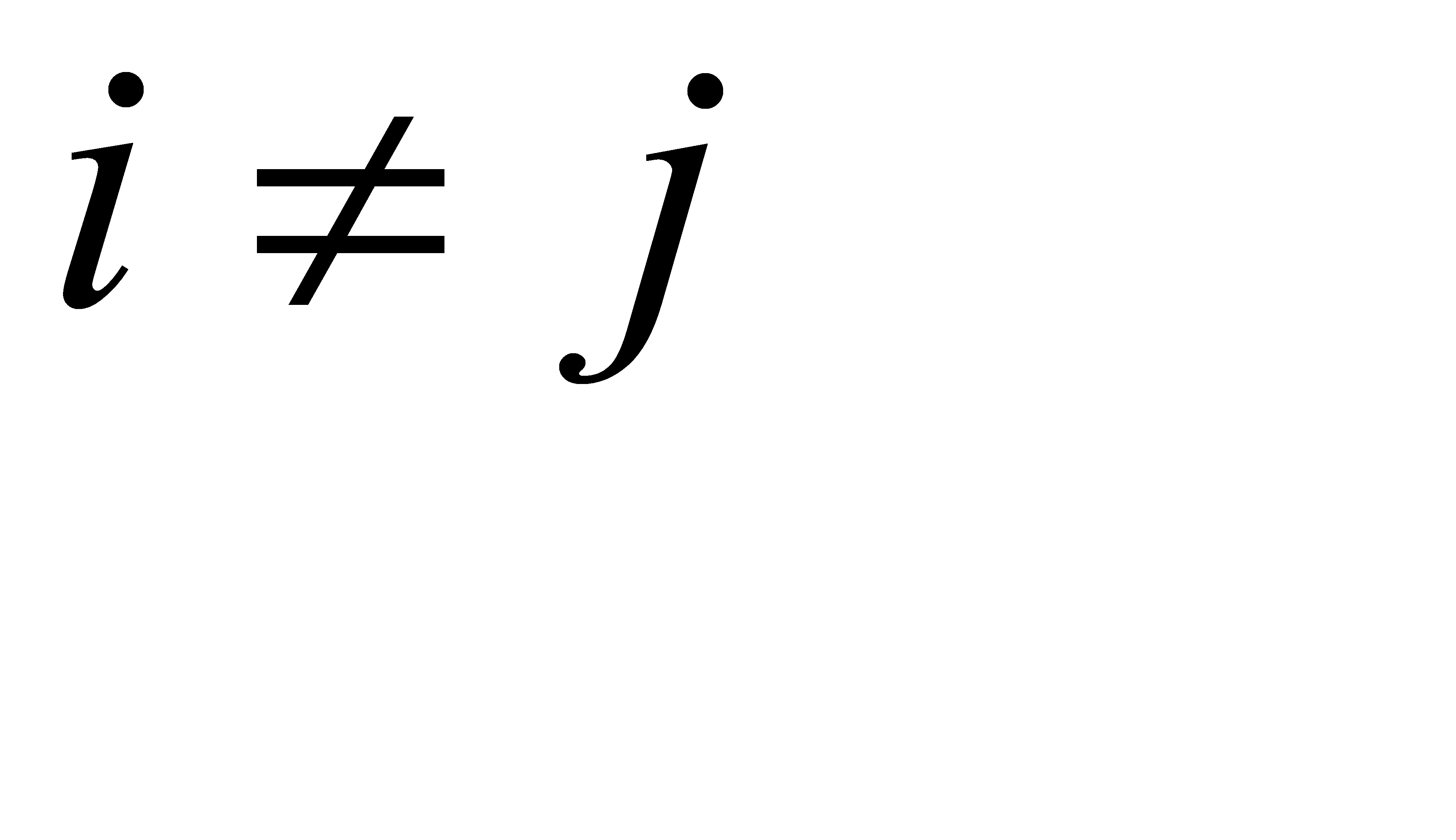и равен при i = j. Правая часть равенства (2.5) представляет собой определитель , в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель . Рассматривая j = 1,2 ,…,n, получим систему, эквивалентную исходной: (2.6). Разделив все уравнения на , найдем единственное решение: .

Предположим теперь, что =0. Тогда система (2.6) примет вид: .

В этом случае, если все =0, система выглядит так: и имеет бесконечно много решений. Если же хотя бы один из система решений не имеет.

Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

2) Если система (2.3) имеет единственное решение, определяемое по формулам: .

3) Если = =0, система имеет бесконечно много решений.

4) Если =0, а хотя бы один из система не имеет решений.

Поиск по сайту: