 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема (Кронекера–Капелли)
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:
Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.
Теорема 1 Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой
Теорема 2 Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.
Таким образом, из сформулированных теорем вытекает способ исследования систем линейных алгебраических уравнений. Пусть n – количество неизвестных,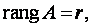 
Тогда:
1) при 
система несовместна;
2) при 
система совместна, причём, если 
, система определённая; если же 
, система неопределённая.
Определение Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Пример. Исследовать систему линейных уравнений
и в случае неопределённости системы найти её базисное решение.
Вычислим ранги основной 
и расширенной матриц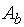 
данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:
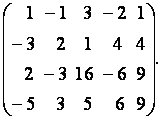
Вторую строку матрицы сложим с её первой строкой, умноженной на 
третью строку – с первой строкой, умноженной на 
а четвёртую строку – с первой, умноженной на 
получим матрицу
К третьей строке этой матрицы прибавим вторую строку, умноженную на 
а к четвёртой строке – первую, умноженную на 
Врезультате получим матрицу
удаляя из которой третью и четвёртую строки получим ступенчатую матрицу
Таким образом, 
Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой. Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений
Неизвестные 
и 
являются главными, а неизвестные 
и 
свободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:
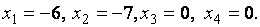
Думаю с этим все понятно.
Билет
1. Вектор. Понятия
Ответ: в геометрическом смысле вектор — это направленный отрезок, обычно определяемый точками своего начала и конца. Так или иначе вектором - называется отрезок, имеющий определенную длину и направление
Основные понятия
1) Модулем вектора |a| в геометрии называется его длина
2) Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направленными строго в противоположные стороны.
3) Ортогональными (перпендикулярными) называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны.
4) Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления.
5) Компланарными называются вектора, которые приведены к одному началу и лежат в одной плоскости. Если хотя бы один из 3 векторов – нулевой, то три вектора тоже компланарны.
6) Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
7) Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
2. Сумма векторов и произведение вектора на число.
Ответ: начнем с простого, чтобы сложить два вектора, достаточно сложить каждую из его координат. Т.е. если есть два вектора с координатами: a (x y z) u b (x1 y1 z1) то их суммой будет:
(x+x1;y+y1;z+z1). С этим ясно, умножение вектора на число тоже довольно просто. Если есть вектор a(x y z) и число b=4, то просто домножаем КАЖДУЮ координату на это число.
3. Условие коллинеарности векторов:
Ответ:
1) Два вектора коллинеарны, если их отношения равны
2) Два вектора коллинеарны, если их векторное пр-е равно нулю.
Пример внизу.
4. Свойства линейных операций над векторами
Сложение векторов коммутативно: 
.
Сложение векторов ассоциативно: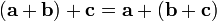 
.
Прибавление нулевого вектора к любому не меняет последнего: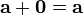 
.
Для любого вектора 
существует вектор 
такой, что 
или 
.
Умножение вектора на число ассоциативно: 
. Умножение вектора на число дистрибутивно относительно сложения чисел: 
.
Дистрибутивность умножения векторов относительно сложения
Умножение вектора на число дистрибутивно относительно сложения векторов: 
.
Очевидно, умножение на единицу не меняет вектор: 
.
Поиск по сайту: