Линейная зависимость и независимость векторов

Система линейно зависима что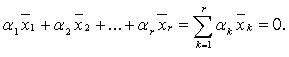

Система линейно независима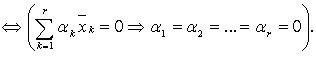

Критерий линейной зависимости векторов

Для того чтобы векторы 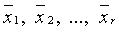(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
Размерность линейного пространства
Линейное пространство V называется n -мерным (имеет размерность n), если в нем:

1) существует n линейно независимых векторов;

2) любая система n + 1 векторов линейно зависима.

Обозначения: n = dim V; .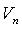

55 Евклидовое пространство.

Определение вещественного евклидова пространства. Вещественное линейное пространство R называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования.
I. Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом (х, у).
П. Указанное правило подчинено следующим четырем аксиомам:
1°. (х, у) = (у, х) (переместительное свойство или симметрия);
2°. (x1 + x2, у) = (х1,у) + (х2, у) (распределительное свойство);
3°. (λх, у) = λ(х, у) для любого вещественного λ;
4°. (х, х) > 0, если х — ненулевой элемент; (х, х) = 0, если х — нулевой элемент.
Подчеркнем, что при введении понятия евклидова пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов, произведения элемента на число и скалярного произведения элементов (важно лишь, чтобы эти правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам скалярного произведения).
Если же природа изучаемых объектов и вид перечисленных правил указаны, то евклидово пространство называется конкретным.

56 Нормируемое пространство.

Линейное пространство называется нормированным, если на нем задана неотрицательная функция , называемая нормой, удовлетворяющая условиям:

1. ;

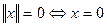2. 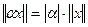для любого и любого числа ;

3. 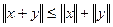для любых 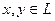(неравенство треугольника).

57 Ортогональное дополнение и его свойства.

58 Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.

|A-ᵡE|=0 - характерестическое уравнение. См Уравнение в вопросе 46(оно характерестическое)

Теорема: Собственными числами матрицы А являются корни уравнения |A-ᵡE|=0 и только они.

Доказательство. Пусть столбец α -- собственный вектор матрицы А с собственным числом ᵡ. Тогда, по определению, Аα=ᵡα. Это равенство можно переписать в виде. Так как для единичной матрицы Е выполнено Еα=α, то Аα-ᵡЕα=0. По свойству матричного умножения (А-ᵡЕ)α=Аα-ᵡЕα и предыдущее равенство принимает вид (А-ᵡЕ)α=0(1) Допустим, что определитель матрицы (А-ᵡЕ) отличен от нуля. Тогда у этой матрицы существует обратная (А-ᵡЕ) в минус первой. Из равенства (1) получим, что α=(А-ᵡЕ)в минус первой×0=0, что противоречит определению собственного вектора. Значит, предположение, что |А-ᵡЕ| неравно нулю, неверно, то есть все собственные числа должны являться корнями уравнения. Пусть ᵡ -- корень уравнения |А-ᵡЕ|=0. Тогда базисный минор матрицы А-ᵡЕ не может совпадать с определителем матрицы и поэтому,Rg(А-ᵡЕ)=r<n, n - порядок матрицы A. Уравнение (1) является матричной записью однородной системы линейных уравнений с неизвестными α1,α2…αn, являющимися элементами матрицы-столбца α. Число решений в фундаментальной системе решений равно n-r, что больше нуля. Таким образом, система (1) имеет хотя бы одно ненулевое решение, то есть числу ᵡ соответствует хотя бы один собственный вектор матрицы A. Определитель |А-ᵡЕ| является многочленом степени n от переменного ᵡ, так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.

59 Линейная функция. Билинейная форма. Квадратичная форма.

60 Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.

61 Линейная балансовая модель.

Пусть рассматривается экономическая система, состоящая из n взаимосвязанных отраслей производства. Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции (первый столбец таблицы 1) и как ее потребитель (первая строка таблицы 1). Обозначим через xi валовый выпуск продукции i-й отрасли за планируемый период и через yi – конечный продукт, идущий на внешнее для

рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т.д.). Таким образом, разность xi - yi составляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Будем в дальнейшем полагать, что баланс составляется не в натуральном, а в

стоимостном разрезе. Одна из задач балансовых исследований заключается в том, чтобы на базе данных об исполнение баланса за предшествующий период определить исходные данные на планируемый период.

62 Модель международной торговли.

В качестве примера математической модели экономического процесса, приводящей к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Процесс взаимных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы. Будем полагать, что бюджеты n стран, которые обозначим соответственно 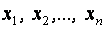, расходуются на покупку товаров.

Пусть 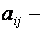доля бюджета 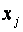, которую j –я страна тратит на закупку товаров у 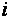-й страны. Введём матрицу коэффициентов :

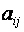. (1)

Тогда, если весь бюджет расходуется только на закупки внутри страны и вне её (это можно трактовать как торговый бюджет), справедливо равенство

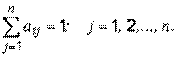(2)

Матрица (1) со свойством (2), в силу которого сумма элементов её любого столбца равна единице, называется структурной матрицей торговли. Для 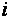-й страны общая выручка от внутренней и внешней торговли выражаетсяформулой 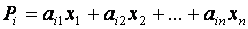. (3)

Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны её бюджет должен быть не больше выручки от торговли, а в силу условия (2) 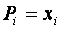или

(4)

Таким образом, условия (4) принимают вид равенств:

. (5)

Введём вектор бюджетов , каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме:

. (6)

Это уравнение означает, что собственный вектор структурной матрицы А, отвечает её собственному значению 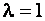, состоит из бюджетов стран бездефицитной международной торговли.

Перепишем уравнение (6) в виде, позволяющем определить :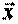

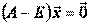
. (7)

63 Комплексные числа. Формула Эйлера. Решение комплексных неравенств на плоскости.

Запись числа z в виде z=x+iy называют алгебраической формой комплексного числа.

Модуль r и аргумент (фи) комплексного числа можно рассматривать как полярные координаты вектора r =ОМ, изображающего комплексное число z=x+iy. Тогда получаем х=rcos(фи), y=r sin(фи). Следовательно, комплексное число z=x+iy можно записать в виде z=r cos(фи)+ir sin(фи) или z=r(cos(фи) +I sin(фи)

Такая запись комплексного числа называется тригонометрической формой.

Модуль r=|z| однозначно определяется по формуле:

R=|z|=x²+y²-все под корнем

Например, |i|=0²+1²(все под корнем)=1. Аргумент фи определяется из формул:

Cos(фи)=x/r sin(фи)=у/r tg(фи)=y/х

При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа z.

Формула Эйлера:

E(в степени i умножить на фи)= cos(фи)+ isin(фи)

Комплексное число z=r(cos(фи)+isin(фи)) можно записать в так называемой показательной (или экспоненциальной) форме z=re в степени iумножить на фи. Где r=|z| - модуль комплексного числа

В силу формулы Эйлера, функция E(в степени i умножить на фи) периодическая с основным периодом 2π. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа.

64 Линейные операторы как отображения. Образ и ядро линейного оператора.

Определение. Если каждому элементу ᵡ из линейного постранства L ставится в соответствие единственный элемент «y» из линейного постранства M, то говорят, что задан оператор, действующий из постранства L в пространство M (или оператор, действующий в пространстве L, если L совпадает с M). Результат действия оператора A на элемент ᵡ обозначают: у=А(х). Над у,х и лямда знаки вектора. Если элементы ᵡ и у связаны соотношением у=А(х), то у называют образом ᵡ; а ᵡ — прообразом у. Множество элементов пространства L, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A). Множество элементов пространства M, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если у=А(х), то х принадлжежит D(A), y принадлжежит Im(A). Ядром оператора называется множество элементов линейного пространства L, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A).

65 Взаимно однозначные отображения.

Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.

Действие оператора обозначают y = A (x), y — образ x, x — прообраз y.

Если каждый элемнт y из Y имеет единственный прообраз x из X, y = A (x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.

Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:

A (u + v) = A (u) + A (v), A (α· u) = α· A (u).

66 Произведение операторов. Обратный оператор.

Пусть А и В – линейные операторы, причем А действует из Е в Е₁, а В действует из Е₁ в Е₂. Произведением ВА операторов А и В называется оператор С, ставящий в соответствие элементу элемент из Е₂.
Область определения D_C оператора С=ВА состоит из тех х 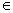D_A, для которых Ах 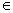D_B. Ясно, что оператор С линеен. Он непрерывен, если А и В непрерывны.
Если А и В – ограниченные операторы, действующие в нормированных пространствах, то и оператор С=ВА – ограничен, причем
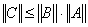(3)
Действительно, , следовательно, выполняется (3).
Сумма и произведение трех и более операторов определяются последовательно. Обе эти операции ассоциативны.
Произведение оператора А на число к (обозначается кА) определяется как оператор, который элементу х ставит в соответствие элемент кАх.
Совокупность Z(E,E₁) всех непрерывных линейных операторов, определенных на всем Е и отображающих Е в Е₁ (где Е и Е₁ – фиксированные линейные нормированные пространства), образует, по отношению к введенным операциям сложения и умножения на число, линейное пространство. При этом Z (E, E₁) – нормированное пространстово (с тем определением нормы оператора, которое было дано выше).
4. Обратный оператор
Пусть А – линейный оператор, действующий из Е в Е₁, и D_A область определения, а R_A – область значений этого оператора.
Определение 6. Оператор А называется обратимым, если для любого у 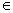R_A уравнение Ах=у имеет единственное решение.
Если А обратим, то любому элементу у 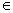R_A можно поставить в соответствие единственный элемент х 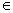D_A, являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным к А и обозначается А^-1.
Теорема 3 [1]. Оператор А^-1, обратный линейному оператору А, также линеен.
Доказательство.

Поиск по сайту: