АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение неравенств на плоскости

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  6. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  7. Арбитражное разрешение международных споров в Древней Греции
  8. Арбитражное разрешение международных споров в Древнем Риме
  9. Б) Правовое разрешение конфликтов
  10. В результате получаем общее решение системы
  11. В. Измерение неравенства доходов
  12. Векторы на плоскости

Множество точек плоскости, координаты которых удовлетворяют неравенству Ax+By+C>0 илиAx+By+C<0, образуют область или множество решений соответствующего неравенства.

Теорема (5). Область решений неравенства Ax+By+C≤0 является полуплоскостью, ограниченная прямой Ax+By+C=0.

Доказательство. Известно, что вектор В каждой из полуплоскостей, ограниченных прямой Ax+By+C=0, отметим по точке: 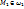и .

На прямой l отметим точку 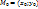, для координат которых:

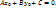
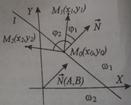Из рисунка видно, что скалярные произведения векторов 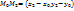, и вектора N, дает неравенства:

 

 

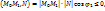
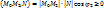
(т.к. – острый и cos >0, – тупой угол и cos <0) или например, для вектора , считая, что точка М – эта любая точка полуплоскости , включая точки прямой l будет выполняться неравенство:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

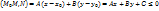
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)