АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Общее уравнение плоскости в пространстве

Читайте также:
  1. A) общее собрание акционеров
  2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  3. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  4. В клинической практике выделяют различные формы афазий, дизартрии, алалию, мутизм и общее недоразвитие речи.
  5. В результате получаем общее решение системы
  6. Векторы на плоскости
  7. ВЛАСТЬ И ВЛИЯНИЕ. ОБЩЕЕ ПОНЯТИЕ. ИСТОЧНИКИ ВЛАСТИ В ОРГАНИЗАЦИИ. ЛИДЕРСТВО И ВЛАСТЬ
  8. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  9. Волна вероятности. Уравнение Шредингера
  10. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  11. Вопрос 1 Корреляционные функции и спектральные плоскости.
  12. Вопрос 24. Сознание – продукт развития материи. Отражение как всеобщее свойство материи. Формы отражения. Сознание как высшая форма отражения.

Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.

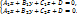
Каждое из уравнений этой системы определяет плоскость. Если плоскости не параллельны (координаты векторов и не пропорциональны), то система определяет прямую L как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (см. рис). Эти уравнения называют общими уравнениями прямой.

Так как прямая L перпендикулярна векторам и , то за направляющий вектор прямой L можно принять векторное произведение


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

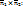
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)