АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема о решении однородной системы линейных уравнений

Читайте также:
  1. I. Формирование системы военной психологии в России.
  2. II. Цель и задачи государственной политики в области развития инновационной системы
  3. II. Экономические институты и системы
  4. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  5. S-M-N-теорема, приклади її використання
  6. SCADA-системы
  7. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  8. TRACE MODE 6: компоненты инструментальной системы
  9. А). Системы разомкнутые, замкнутые и комбинированные.
  10. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  11. Абиотические компоненты экосистемы.
  12. Абстрактные линейные системы

Теорема (о линейном решении однородных систем).
Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы.

Теорема (о структуре общего решения).
Пусть 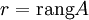, тогда:

· если , где — число переменных системы, то существует только тривиальное решение;

· если , то существует линейно независимых решений рассматриваемой системы: , причём её общее решение имеет вид: , где — некоторые константы.


Теорема (об общем решении неоднородных систем).
Пусть ,тогда:

· если , где — число переменных системы, то решение (2) существует и оно единственно;

· если , то общее решение системы (2) имеет вид , где — общее решение системы (1), называемое общим однородным решением, — частное решение системы (2), называемое частным неоднородным решением.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)