Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами

Скалярным произведением векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними. Если хоть один из векторов нулевой, то скалярное произведение по определению считают равным нулю. , –угол между векторами a и b.

1. Скалярное произведение произвольного вектора а на себя же всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор - нулевой.

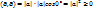
2. Скалярное произведение любых перпендикулярных векторов a и b равно нулю.

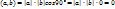
3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них - нулевой.

4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.

5. Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.

Свойства скалярного произведения:

1. (a,b)=(b,a)- симметричность.

2. 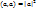– скалярный квадрат.

3. Если 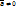, то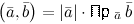

4. Если и и (a,b)=0, то . Верно и обратное утверждение.

5.

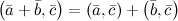
6.

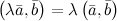
7.

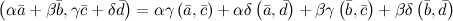
Если векторы и заданы своими координатами: , , то их скалярное произведение вычисляется по формуле:

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

Поиск по сайту: