АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

В результате получаем общее решение системы

Читайте также:
  1. A) общее собрание акционеров
  2. I. Решение логических задач средствами алгебры логики
  3. I. Формирование системы военной психологии в России.
  4. II. Решение логических задач табличным способом
  5. II. Цель и задачи государственной политики в области развития инновационной системы
  6. II. Экономические институты и системы
  7. III. Разрешение споров в международных организациях.
  8. III. Решение логических задач с помощью рассуждений
  9. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  10. А). Системы разомкнутые, замкнутые и комбинированные.
  11. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  12. Абиотические компоненты экосистемы.

.

Одно базисное решение получаем при x4=x5=0, т.е. x1=3,5; x2=0,5; x3=3 или X1=(3,5; 0,5; 3; 0; 0).

Чтобы получить другое базисное решение, достаточно задать x4=1; x5=0, тогда x1=6; x2=1; x3=2 или X2=(6; 1; 2; 1; 0).

 

Пример 6. Вычислить пределы функций, не пользуясь правилом Лопиталя:

а) ;

Функция не определена при х=5 и поэтому разрывна в этой точке. Числитель и знаменатель в точке х=5 обращается в нуль, налицо неопределенность . Выделим общий множитель (х-5) и сократим на него числитель и знаменатель, считая х ¹ 5, х ® 5.

.

б) ;

Ни числитель, ни знаменатель этой дроби не имеют конечного предела так как они неограниченно возрастают при неограниченном возрастании х, т. е. имеем дело с неопределенностью . Поделим числитель и знаменатель дроби на х2:

так как , , , при х ® ¥ – величины бесконечно малые.

в) ;

Поскольку числитель и знаменатель обращаются в нуль при х=0, то имеем дело с неопределенностью вида .

Воспользуемся тригонометрической формулой для преобразования знаменателя 2sin2x=1-cos2x и получим предел, в котором участвует тригонометрическая функция sinx.

Применив первый замечательный предел 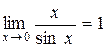, получаем:

,

так как при х ® 0.

г) .

Предел функции при х ® 0 равен единице, т.е. в данном примере требуется раскрыть неопределенность . Примеры такого вида сводятся ко второму замечательному пределу .

Преобразуем выражение в скобках к виду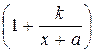

.

Тогда

,

т. к. , .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)