 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Средствами матричного исчисления
Решение: Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу ее расширенной матрицы, т. е. r (A) =r (A1), где
, 
.
Расширенная матрица системы имеет вид:
.
Умножим первую строку на (–3),а вторую на (2); прибавим после этого элементы первой строки к соответствующим элементам второй строки; вычтем из второй строки третью. В полученной матрице первую строку оставляем без изменений.
~
Разделим элементы третьей строки на (6) и поменяем местами вторую и третью строки:
~ 
~
Умножим вторую строку на (–11) и прибавим к соответствующим элементам третьей строки.
~ 
Разделим элементы третьей строки на (10).
~ 
; 
~ 
.
Найдем определитель матрицы А.
.
Следовательно, r (A) =3. Ранг расширенной матрицы r (A1) так же равен 3, т.е.
r (A) =r (A1)= 3 Þ система совместна.
1) Исследуя систему на совместность, расширенную матрицу преобразовали по методу Гаусса.
Метод Гаусса состоит в следующем:
1. Приведение матрицы к треугольному виду, т. е. ниже главной диагонали должны находиться нули (прямой ход).
2. Из последнего уравнения находим х3 и подставляем его во второе, находим х2, и зная х3, х2 подставляем их в первое уравнение, находим х1 (обратный ход).
Запишем, преобразованную по методу Гаусса, расширенную матрицу
~
в виде системы трех уравнений:
Þ х3=1
х2=х3 Þ х3=1
2х1=4+х2+х3 Þ 2х1=4+1+1 Þ
Þ 2х1=6 Þ х1=3
Ответ: х1=3, х2=1, х3=1.
2) Решим систему по формулам Крамера: если определитель системы уравнений Δ отличен от нуля, то система имеет единственное решение, которое находится по формулам
; 
; 
.
Вычислим определитель системы Δ:
Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители Δ1, Δ2, Δ3. Они получаются из определителя системы Δ заменой соответствующего столбца на столбец свободных коэффициентов.
Находим по формулам неизвестные:
; 
; 
Ответ: х1=3, х2=1, х3=1 .
3) Решим систему средствами матричного исчисления, т. е. при помощи обратной матрицы.
А×Х=В Þ Х=А-1× В, где А-1 – обратная матрица к А,
- столбец свободных членов,
- матрица-столбец неизвестных.
Обратная матрица считается по формуле:
(*)
где D - определитель матрицы А, Аij – алгебраические дополнения элемента а ij матрицы А. D = 60 (из предыдущего пункта). Определитель отличен от нуля, следовательно, матрица А обратима, и обратную к ней матрицу можно найти по формуле (*). Найдем алгебраические дополнения для всех элементов матрицы А по формуле:
Аij= (-1) i+j Mij .
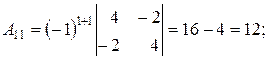
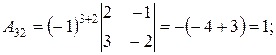
Запишем обратную матрицу.
.
Сделаем проверку по формуле: А-1× А=Е.
А-1А =
Вывод: так как произведение А-1× А дает единичную матрицу, то обратная матрица А-1 найдена верно и решение системы определяется по формуле Х=А-1×В.
.
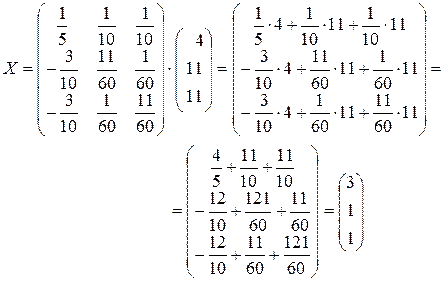Ответ: х1=3, х2=1, х3=1.
Проверка. Подставим полученные значения в систему. Получим:
Т. к. неизвестные х1, х2, х3 обратили каждое уравнение в тождество, то они найдены верно.
Пример 6. Решить систему методом Гаусса и найти какие-нибудь два базисных решения системы.
Решение:
Поиск по сайту: