Пример 7. а) Найти производную функции

а) Найти производную функции .

Решение:

Сначала преобразуем данную функцию:

б) Найти производную функции .

Решение:

в) Найти производную функции .

Решение:

Пример 8. Исследовать функцию и построить график.

Решение.

1. Данная функция не определена при , т. к. в этой точке знаменатель обращается в ноль. Значит

.

2. , 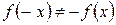. Следовательно, функция общего вида.

3. Не периодична.

4. Точки пересечения с осью Ох: при , . С осью Оу: ,

. Нашли две точки пересечения графика функции с осями координат: и .

5. Исследуем на непрерывность. Точкой разрыва является .

6. Из предыдущего пункта следует, что - вертикальная асимптота.

Найдем наклонную асимптоту .

. .

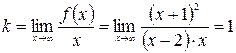Итак, - наклонная асимптота.

7. Исследуем на возрастание, убывание и экстремум функции. Для этого найдем производную функции.

.

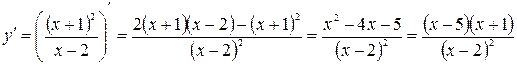Найдем точки, в которых производная равна нулю .

и .

Далее отметим данные точки на числовой оси и к ним добавляем точку , в которой не определена.

Находим интервалы, на которых : и

: .

При прохождении точки производная меняет знак с плюса на минус. Следовательно, - точка экстремума функции, а именно максимум.

.

При прохождении точки производная меняет знак с минуса на плюс. Следовательно, так же является точкой экстремума функции, а именно минимумом.

.

8. Исследуем на вогнутость функции и точки перегиба. Для этого находим производную второго порядка.

.

Вторая производная в ноль никогда не обращается, поэтому на числовой оси отмечаем только .

: - функция вогнута и : - выпукла. Точек перегиба нет.

Составим таблицу, в которую занесем полученные сведения.

х		-1
	+		-	не сущ.	-		+
	-		-	не сущ.	+		+
у				верт. ас.

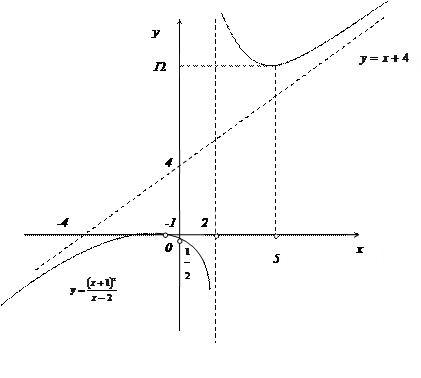
После того, как собрали все данные, полученные в ходе исследования, изобразим характерное поведение графика данной функции. (См. рис.).

Поиск по сайту: