 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Исследовать функции методом дифференциального исчисления и схематично построить их графики
71. а)  ;
;
72. а)  ;
;
73. а)  ;
;
74. а)  ;
;
75. а)  ;
;
76. а)  ;
;
77. 
78. 
79. 
80. 
Решение типового варианта
Пример 1. Вычислить определители:
а)  ; б)
; б)  .
.
Решение:
Определитель равен сумме произведений элементов какой−либо строки или столбца на их алгебраические дополнения:  . Алгебраическим дополнением
. Алгебраическим дополнением  некоторого элемента определителя называется минор этого элемента, умноженный на (−1)S, где
некоторого элемента определителя называется минор этого элемента, умноженный на (−1)S, где  – сумма номеров строки и столбца, на пересечении которых стоит данный элемент. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
– сумма номеров строки и столбца, на пересечении которых стоит данный элемент. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Выберем в рассматриваемом определителе любую строку. Например, первую строку. Тогда определитель может быть вычислен по формуле


 где
где  − минор элемента
− минор элемента 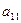 , полученный вычеркиванием из исходного определителя первой строки и первого столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и первого столбца, на пересечении которых находится элемент 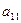 :
: 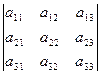 ,
,


 − минор элемента
− минор элемента 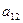 , полученный вычеркиванием из исходного определителя первой строки и второго столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и второго столбца, на пересечении которых находится элемент 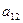 :
: 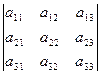 ,
,


 − минор элемента
− минор элемента  , полученный вычеркиванием из исходного определителя первой строки и третьего столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и третьего столбца, на пересечении которых находится элемент  :
:  .
.
Выполним задание для первого определителя:
М22 =  = (−1) × (−1) – 0 × 0 = 1 – 0 = 1,
= (−1) × (−1) – 0 × 0 = 1 – 0 = 1,
А23 = (−1)2+3 × М23 = (−1) × ((−1)×5 − 2×0) = 5.
Вычислим определитель, разложив его по элементам первой строки: 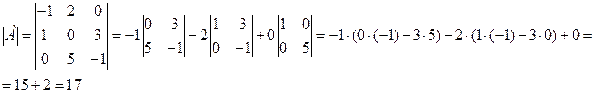 .
.
б) Выполним задание для второго определителя, раскрывая все определители по элементам первой строки:
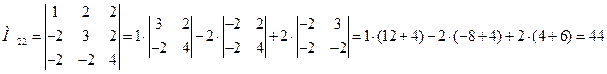

 .
.
Полученные определители третьего порядка сведем к определителям второго порядка, еще раз разложив каждый из них по первой строке.
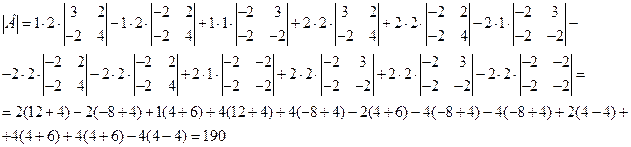 Ответ: а)
Ответ: а)  ,
, 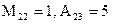 ; б)
; б)  ,
,  .
.
Пример 2. Даны матрицы  и
и  . Вычислить
. Вычислить  и
и  , если они существуют.:
, если они существуют.:
а) 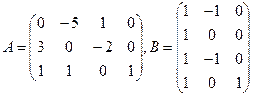 ;
;
Решение:

определим размер матрицы, которую получим в результате умножения: первая матрица имеет размер  , вторая −
, вторая −  . Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер
. Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер  .
.
Для того, чтобы найти элемент  необходимо
необходимо  − ю строку первой матрицы умножить скалярно на
− ю строку первой матрицы умножить скалярно на 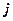 −й столбец второй матрицы
−й столбец второй матрицы

 Ответ:
Ответ:  ;
;  .
.
Пример 3. Определить, имеет ли данная матрица обратную, найти обратную матрицу к данной  .
.
Решение:
Обратную матрицу к данной матрице  будем находить по следующему плану:
будем находить по следующему плану:
1. Вычислим определитель матрицы 
2. Вычислим алгебраические дополнения для всех элементов матрицы  по формуле
по формуле
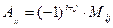 ,где
,где  минор элемента
минор элемента  матрицы
матрицы  .
.
3. Запишем матрицу  , элементами которой являются соответствующие алгебраические дополнения
, элементами которой являются соответствующие алгебраические дополнения
4. Найдем транспонированную матрицу 
5. Найдем обратную матрицу по формуле 


1. Вычислим определитель матрицы  по формуле
по формуле


2. Вычислим алгебраические дополнения для всех элементов матрицы 

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  первую строку и первый столбец)
первую строку и первый столбец)
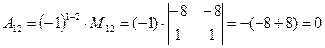
(для вычисления минора 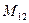 вычеркиваем в матрице
вычеркиваем в матрице  первую строку и второй столбец)
первую строку и второй столбец)

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  первую строку и третий столбец)
первую строку и третий столбец)

(для вычисления минора 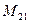 вычеркиваем в матрице
вычеркиваем в матрице  вторую строку и первый столбец)
вторую строку и первый столбец)

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  вторую строку и второй столбец)
вторую строку и второй столбец)

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  вторую строку и третий столбец)
вторую строку и третий столбец)

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  третью строку и первый столбец)
третью строку и первый столбец)

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  третью строку и второй столбец)
третью строку и второй столбец)

(для вычисления минора  вычеркиваем в матрице
вычеркиваем в матрице  третью строку и третий столбец)
третью строку и третий столбец)
3. Запишем матрицу  , элементами которой являются найденные алгебраические дополнения
, элементами которой являются найденные алгебраические дополнения

4. Найдем транспонированную матрицу  (строки становятся столбцами, а столбцы – строками с сохранением порядка)
(строки становятся столбцами, а столбцы – строками с сохранением порядка)


5. Найдем обратную матрицу



Произведем проверку. Для этого найдем произведения  и
и 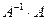 . Если окажется, что они равны
. Если окажется, что они равны  , то матрица
, то матрица  найдена верно.
найдена верно.
Имеем
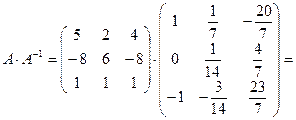
определим размер матрицы, которую получим в результате умножения: первая матрица имеет размер  , вторая −
, вторая −  . Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер
. Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер  .
.
Для того, чтобы найти элемент  необходимо
необходимо  − ю строку первой матрицы умножить скалярно на
− ю строку первой матрицы умножить скалярно на  −й столбец второй матрицы
−й столбец второй матрицы
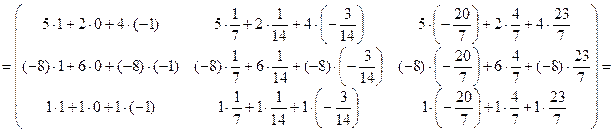

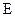 .
.
аналогично находим произведение 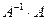 :
:



Ответ: 
Пример 4. Даны координаты вершин пирамиды ABCD: A(10; 6; 6), B(- 2; 8; 2), C(6; 8; 9), D(7; 10; 3).
Найти:
1) Длину ребра АВ;
2) Угол между ребрами АВ и АD;
3) Уравнение прямой АВ;
4) Уравнение плоскости АВС;
Поиск по сайту: