Аналитические функции

Определение 2.1. Функция называется аналитической в точке , если существует такое 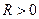, что в круге она представима степенным рядом вида (1.1), т.е. существуют такие комплексные числа 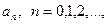что

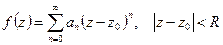, (2.1)

Сумма, разность и произведение аналитических в точке функций снова является аналитической в этой точке функцией.

Лемма 1. Если

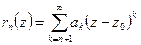
- остаток сходящегося ряда (2.1) с положительным радиусом сходимости , то

при , (2.2)

и, значит,

при , (2.3)

Теорема 5. Представление аналитической в точке функции в виде степенного ряда (2.1) единственно, т.е. если

, (2.4)

то

.

Теорема 6. Если 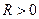- радиус сходимости степенного ряда

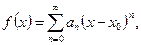(2.5)

то:

1) функция имеет в интервале производные всех порядков, которые находятся из ряда (2.5) почленным дифференцированием;

2) для любого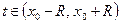

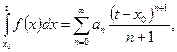
т.е. внутри интервала сходимости степенной ряд можно почленно интегрировать;

3) степенные ряды, получающиеся из ряда (2.5) в результате почленного дифференцирования или интегрирования, имеют тот же радиус, что и сам ряд (2.5).

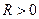Теорема 7. Если функция аналитическая в точке , т.е. представима в окрестности этой точки рядом (2.5) с радиусом сходимости , то

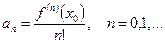, (2.6)

т.е.

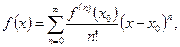
Поиск по сайту: