Знакопеременные ряды. В этом пункте рассматриваются ряды с вещественными членами, знаки которых, вообще говоря, изменяются при изменении номера; такие ряды называются

В этом пункте рассматриваются ряды с вещественными членами, знаки которых, вообще говоря, изменяются при изменении номера; такие ряды называются знакопеременными рядами.

Рассмотрим прежде всего так называемые знакочередующиеся ряды, т.е. ряды, члены которых поочередно то положительны, то отрицательны.

Теорема 1 (Лейбница). Если

(1.1)

и

n= 1,2, …, (1.2)

то знакочередующийся ряд

(1.3)

сходится.

Д о к о з а т е л ь с т в о. Рассмотрим частичные суммы четного порядка ряда (1.3):

Их можно записать в виде

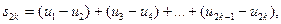k = 1,2, …

В условиях (1.2) выражения в круглых скобках неотрицательны и потому т.е. последовательность частичных сумм четного порядка ряда (1.3) монотонно возрастает.

Замечая, что частичные суммы можно записать также в виде

k = 1,2, …

и что выражения в круглых скобках в силу условия (1.2) неотрицательны, а получаем, что т.е последовательность 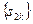ограничена сверху.

Из монотонного возрастания и ограниченности сверху последовательности 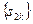следует, что она сходится.

Пусть

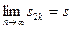. (1.4)

Покажем, что частичные суммы нечетного порядка ряда (1.3) стремится к тому же пределу. Действительно,

k = 1,2. …. (1.5)

и так как, согласно (1.1)

то в силу (1.4) и (1.5) имеем

(1.6)

Из (1.4) и (1.5) следует, что

Теорема доказана.

Следствие. Любая частичная сумма 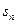ряда (1.1) отличается от его суммы s на величину, меньшую следующего члена , иначе говоря, абсолютная величина остатка ряда в этом случае не превышает абсолютной величины его первого члена, т.е

Действительно из неравенства следует, что

,

,

k = 1, 2, ….

Следствие доказано.

Поиск по сайту: