Свойства равномерно сходящихся рядов и последовательностей

Теорема3.1. Если функция , непрерывны на множестве и ряд

равномерно сходится на , то его сумма

также непрерывна на .

Теорема3.1’. Если функция , непрерывны на множестве и на , то непрерывна на .

Это означает, что для любой точки

,

т.е. пределы по и по можно переставлять.

Действительно, предел последовательности , является в силу теоремы 3.1’ непрерывной на множестве функцией, поэтому левая часть равенства равна :

.

Перестановочность указанных пределов доказана.

Теорема3.2. Пусть функции , непрерывны на отрезке и ряд

(3.1)

равномерно сходится на , тогда какова бы ни была точка , ряд

(3.2)

также равномерно сходится на , и если

, (3.3)

то

, . (3.4)

Если эту формулу переписать в виде

,

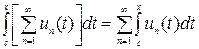то видно, что она означает законность в условиях теоремы (3.1) почленного интегрирования ряда.

Теорема3.2’. Если последовательность непрерывных на отрезке функций , равномерно на этом отрезке сходится к функции , то, какова бы ни была точка ,

на ,

в частности,

.

Перейдем теперь к вопросу о дифференцировании рядов.

Теорема3.3. Пусть функции , непрерывно дифференцируемы на отрезке и ряд, составленный из их производных

(3.5)

равномерно сходится на отрезке . Тогда если ряд

сходится хотя бы в одной точке , то он сходится на всем отрезке , его сумма

(3.6)

непрерывно дифференцируема и

. (3.7)

Если эту формулу записать в виде

,

то видно, что она означает законность при сделанных предложениях почленного дифференцирования ряда.

Литература: 1, с.67-97; 7, с. 419 – 447; 10, с. 540 -561

Контрольные вопросы:

1. Какую последовательность называют функциональной последовательностью?

2. Какой ряд называют функциональным рядом?

3. Сформулируйте определение функциональной последовательности (ряда) сходящейся в точке, на множестве.

4. Какой ряд называют абсолютно сходящимся на множестве?

5. Сформулируйте определения равномерно сходящейся последовательности (ряда) на множестве.

6. Сформулируйте и докажите критерий Коши сходимости последовательностей и рядов.

7. Сформулируйте признак Вейерштрасса равномерной сходимости последовательностей и рядов.

8. Сформулируйте и докажите признаки Дирихле и Абеля равномерной сходимости рядов.

Поиск по сайту: