Признаки сравнения

В этом пункте мы установим ряд признаков, позволяющих сделать заключение о сходимости (или расходимости) рассматриваемого ряда посредством сравнения его с другим рядом, сходимость (или расходимость) которого известна.

Теорема 2. Пусть 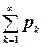и -два ряда с неотрицательными членами. Пусть далее, для всех номеров k справедливо неравенство

(2.1)

Тогда сходимость ряда влечет за собой сходимость ряда 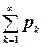, расходимость ряда 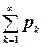влечет за собой расходимость ряда .

Доказательство. Обозначим n -е частичные суммы рядов 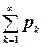и соответственно через S_n и Последнее неравенство означает, что ограниченность последовательности частичных сумм{ }влечет за собой ограниченность последовательности частичных сумм{S_n}и, наоборот, неограниченность последовательности частичных сумм {S_n} влечет за собой неограниченность последовательности частичных сумм{ }. В силу теоремы 1 теорема 2 доказана.

Следствие из теоремы 2. Если ряд 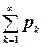- с неотрицательными членами, ряд со строго положительными членами и если существует конечный предел

то сходимость ряда влечет за собой расходимость ряда .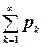

Теорема 3. Пусть 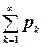и два ряда со строго положительными членами. Пусть далее для всех номеров k справедливо неравенство

. (2.2)

Тогда сходимость ряда влечет за собой сходимость ряда 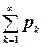, расходимость ряда 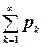влечет за собой расходимость ряда .

Доказательство. Запишем неравенство (2.2) для k=1,2,...,n-1, где n –любой номер

Перемножая почленно все написанные неравенства, получим

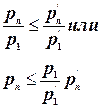
Поскольку в последнем неравенстве величина представляет собой положительную постоянную, не зависящую от номера n. Теорема 3 доказана.

Поиск по сайту: