О перестановке членов абсолютно сходящихся рядов

. Докажем, что для всякого абсолютно сходящегося ряда справедливо переместительное свойство

Теорема4 (Коши). Если данный ряд сходится абсолютно, то любой ряд, полученный из данного посредством некоторой перестановки членов, также сходится абсолютно и имеет ту же сумму, что и данный ряд.

Д о к а з а т е л ь с т в о. Пусть ряд

(4.1)

сходится абсолютно и сумма ряда равна S. Пусть, далее,

(4.2)

ряд, полученный из ряда (4.1) посредством некоторой перестановки членов. Требуется доказать, что: 1) ряд (4.2) сходится и имеет сумму, равную S; 2) ряд (4.2) сходится абсолютно. Докажем сначала 1). Достаточно доказать, что для любого найдется номер N такой, что при

(4.3)

Фиксируем произвольные . Так как ряд (4.1) сходится абсолютно и имеет сумму, равную S, то для выбранного можно указать номер такой, что будут справедливы неравенства

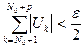(p – любое натуральное число) (4.4)

и

. (4.5)

Выберем теперь номер N столь большим, чтобы любая частичная сумма ряда (4.2) с номером n, превосходящим N, содержало все первые членов ряда (4.1).

Оценим разность, стоящую в левой части (4.3), и докажем, что при для этой разности справедливо неравенство (4.3). В самом деле, указанную разность можно представить в виде

. (4.6)

Так как модуль суммы двух величин не превосходит суммы их модулей, то из (4.6) получим

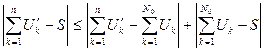. (4.7)

Из неравенства (4.5) и (4.7) очевидно, что для доказательства неравенства (4.5) достаточно доказать, что при

. (4.8)

Для доказательства неравенства (4.8) заметим, что при первая из сумм, стоящих в его левой части, содержит все первых членов ряда (4.1). Вследствие этого разность

(4.9)

представляет собой сумму членов ряда (4.1) с номерами, каждый из которых превосходит .

Если выбрать натуральное столь большим, чтобы номер превосходило номера всех членов только что указанной суммы, то для разности (4.9) во всяком случае справедливо неравенство

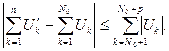(4.10)

Из неравенства (4.10) и (4.4) вытекает неравенство (4.8). Тем самым доказано неравенство (3.3), т.е. доказано, что ряд (4.2) сходится и имеет сумму равную S. Остается доказать утверждение «0 о том, что ряд (4.2) сходится абсолютно. Доказательство этого утверждения следует из утверждения 1), если его применить к рядам

и 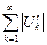. (4.11)

При этом мы докажем сходимость второго из рядов (4.11), т.е. докажем абсолютную сходимость ряда (4.2). Теорема полностью доказана

Литература: 1,с.28-35; 7, с.293-300; 10, с.524-532

Контрольные вопросы:

1. Какой ряд называют абсолютно сходящимся?

2. Какой ряд называют условно сходящимся?

3. Исследуйте на абсолютную сходимость ряд .

4. Сформулируйте и докажите теорему Римани.

5. Сформулируйте и докажите теорему Коши.

6. Какой ряд называют знакопеременным?

7. Какой ряд называют знакочередующимся?

8. Сформулируйте и докажите признак Коши.

Поиск по сайту: