Разложение элементарных функций в ряд Тейлора

Прежде всего, найдем разложение в ряд некоторых основных элементарных функций.

Разложение в ряд функции .

Так как , то для любого фиксированного при всех и всех

,

Таким образом, условия теоремы 8 выполнены , поэтому функция раскладывается в ряд Тейлора на любом конечном интервале, а значит и на всей вещественной оси. Поскольку в данном случае , то это разложение имеет вид

, (4.1)

напомним, что было установлено, что ряд

абсолютно сходится на всей комплексной плоскости. Мы видим теперь, что для вещественных его сумма равна . В случае существенно комплексных его сумму по аналогии обозначают 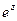; таким образом, формула

, (4.2)

для комплексных является определением функции .

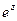Разложение в ряд 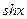и .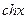

Заменяя в формуле (4.1) на 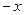(это означает просто изменение обозначения), получим

, (4.4)

, (4.5)

В правых частях этих формул в силу единственности разложения функций в степенные ряды стоят ряды Тейлора функци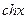й и .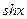

Разложение в ряд и 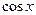. Формулы Эйлера.

Если , то , поэтому для всех вещественных . Согласно теореме 8 отсюда следует, что функция раскладывается в степенной ряд на всей вещественной оси. Вспоминая формулу Тейлора для синуса, получим для него ряд Тейлора для

, (4.6)

Рассуждая аналогично и вспоминая формулу Тейлора для косинуса, получим для него ряд Тейлора

, (4.7)

также сходящийся на всей вещественной оси.

Разложение в ряд функции .

Формула Тейлора для имеет вид

.

Запишем остаточный член в формуле Лагранжа. Замечая, что

,

получим

,

Если

,

то

,

и поэтому

и, в частности,

, (4.8)

Если же , то целесообразно записать остаточный член в форме Коши:

.

В этом случае

и

,

поэтому

,

откуда при также получаем (4.8).

Таким образом,

, (4.9)

для всех .

При ряд, стоящий в правой части равенства (4.9), отличается от гармонического ряда лишь множителем -1 и поэтому расходится. Расходится он также и при всех таких, что , ибо в этом случае -й член ряда (4.9) не стремится к нулю, боле того

.

Разложение в ряд бинома .

.

Литература: 1, с. 540 -561; 7, с. 102-117; 10, с. 561-588

Контрольные вопросы и задания:

1. Какой ряд называют степенным?

2. Сформулируйте и докажите теорему Абеля о сходимости степенного ряда.

3. Сформулируйте определение радиуса сходимости ряда.

4. Сформулируйте определение круга сходимости ряда.

5. Запишите формулу Коши-Адамара.

6. Какие функции называются аналитическими?

7. При каких условиях степенной ряд можно почленно дифференцировать и интегрировать?

8. Какой ряд называют рядом Тейлора?

9. Запишите разложения в ряд Тейлора функции: , , , , , , .

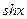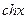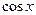Поиск по сайту: