 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Б) Вычисление тригонометрических функций
Значение тригонометрических функций можно вычислять с помощью рядов (2. - 3. § 9)

Эти ряды знакочередующиеся и сумма их не больше первого члена (см. §3).
Впервые эти формулы были получены Ньютоном. Они наиболее удобны для вычисления приближенных значений sin x и cos х при
| x | < 1 в силу быстрой сходимости данных рядов. Если же | х | ³ 1, то целесообразно использовать формулы приведения и свести задачу вычисления sin x или cos х для х Î 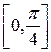 . Более того, если нам известны значения этих функций до
. Более того, если нам известны значения этих функций до  , то значения до
, то значения до 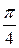 могут быть найдены из равенств
могут быть найдены из равенств
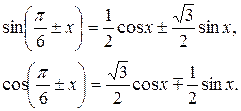
Вычислим, например, cos 5о с точностью до 10- 5. Переведем градусы в радианы:
 .
.
Следовательно, подставляя в ряд cos х, получаем:
 ,
,
отсюда,  .
.
в) Вычисление значений радикалов.
Для вычисления значений радикалов (корней) очень удобна формула (биномиальный ряд 5. §9):
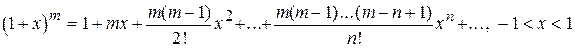 .
.
Вычислим  с точностью до 0,0001.
с точностью до 0,0001.
Получаем:  .
.
Поэтому имеем:
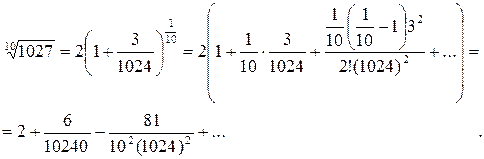
Получили знакочередующийся ряд.

Итак, с точностью до 10- 4 получаем:
 .
.
Замечание. Можно дать формулу преобразования корня любой степени в общем виде.
Пусть требуется вычислить  .
.
Подберем какое-либо не очень точное, но известное приближение
заданного корня, например,  » с. Отсюда следует, что
» с. Отсюда следует, что  . Тогда, очевидно, справедливо равенство:
. Тогда, очевидно, справедливо равенство:
 ,
,
где a - некоторая малая величина.
Отсюда получаем:
 .
.
Следовательно,
 .
.
Разлагая теперь полученное выражение в биномиальный ряд, мы будем иметь приближенную формулу, причем любой точности.
Итак, получаем:
 .
.
Например,
 ,
,
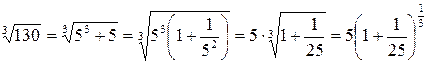 ,
,
 ,
,
 .
.
г) Показательные функции.
Для вычисления значений показательной функции используется ряд (1 § 9):
 .
.
Очевидно, чем меньше х, тем быстрее сходится ряд.
Вычислим 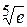 с точностью 0,0001.
с точностью 0,0001.
Получаем:
 ,
,
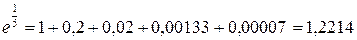 ,
,
т.к.

Следовательно,
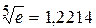 .
.
Поиск по сайту: