Положительные ряды

Ряд (1) называется положительным, если среди его среди его членов нет неотрицательных.

Частичные суммы положительного ряда образуют возрастающую последовательность

.

Следовательно, положительный ряд (1) всегда имеет сумму, причем конечную, если ряд сходится и бесконечную, если ряд расходится.

Используя теорему о пределе монотонной переменной, получаем основное утверждение, а именно:

Теорема 1. (Критерий сходимости положительных рядов). Для сходимости положительного ряда необходимо и достаточно, чтобы последовательность его частичных сумм была ограниченной.

Действительно, так как последовательность частичных сумм положительного ряда монотонно возрастает, то для её сходимости необходимо и достаточно, чтобы она была ограничена.

На практике этим признаком пользоваться очень сложно. Но используя эту теорему легко доказать ряд достаточных признаков сходимости положительных рядов. Сформулируем их.

Теорема 2. (Признак сравнения). Пусть даны два положительных ряда и и выполняются неравенства а_п £ b_n хотя бы начиная с некоторого номера N, т.е. для всех п > N. Тогда из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Иногда на практике более удобна следующая теорема, вытекающая из предыдущей.

1. Предельный признак сравнения числовых рядов.

2. Признаки Коши. Признак Даламбера.

3. Знакочередующиеся и знакопеременные ряды.

4. Признак Лейбница.

5. Абсолютная и условная сходимость.

1. Теорема 1. (Предельный признак сравнения). Пусть даны два положительных ряда и . Если существует конечный, отличный от нуля предел , то оба ряда либо одновременно сходятся, либо расходятся.

Рассмотрим примеры установления сходимости или расходимости рядов с использованием признаков сравнения.

Замечание 1. При исследовании рядов на сходимость по теоремам сравнения, как правило, для сравнения используют либо бесконечно убывающую геометрическую прогрессию, либо обобщенный гармонический ряд , который сходится при a > 1 и расходится при a £ 1 (его иногда называют рядом Дирихле).

Замечание 2. Если общий член ряда является дробно-рациональной функцией, т.е. вида , где Р_к (п) и Q_т (п) - многочлены степени к и т соответственно, то для сравнения рекомендуем использовать ряд , где a = т - к, т.е. от степени знаменателя вычитаем степень числителя.

2. Теорема 2 (Радикальный признак Коши). Пусть дан ряд и существует предел

.

Тогда при С < 1 ряд сходится; при С > 1 ряд расходится.

Следует заметить, что при С = 1 как и в предыдущем случае необходимо применить другой признак, например, сравнения.

Пример. Исследовать на сходимость ряд .

Решение. Находим:

.

Так как , то данный ряд сходится.

Пример. .

Решение.

.

Следовательно, ряд сходится.

Пример. .

Решение.

.

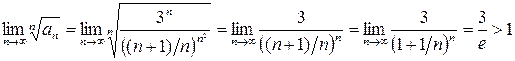Следовательно, данный ряд расходится.

Теорема 3. (Признак Даламбера). Пусть дан ряд , а_п >0 и существует предел . Тогда при D < 1 ряд сходится; при D > 1 ряд расходится.

Замечание 3. При D = 1 признак Даламбера не дает ответа, т.к. в этом случае существуют примеры как сходящихся, так и расходящихся рядов.

Пример. Исследуем на сходимость ряд .

Решение. Находим: , ,

Так как , то ряд расходится.

Пример. .

Решение. ,

.

Ряд расходится.

Поиск по сайту: