Указания. Следует иметь в виду, что среди достаточных признаков сходимости рядов с положительными членами наиболее эффективным является интегральный признак Коши

Следует иметь в виду, что среди достаточных признаков сходимости рядов с положительными членами наиболее эффективным является интегральный признак Коши. Поэтому, если другие признаки не позволяют решить вопрос о сходимости или расходимости числового ряда с положительными членами, то следует прибегнуть к интегральному признаку Коши.

Задача 1. Исследовать на сходимость ряд

а) пользуясь признаком Даламбера;

б) пользуясь интегральным признаком.

Решение: а) по условию

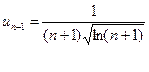
следовательно,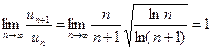

и, значит, признак Даламбера не позволяет сделать заключения о сходимости или расходимости ряда.

б) члены данного ряда положительны и убывают; в качестве функции f (х) в интегральном признаке возьмем функцию f (x) = 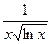при х 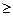2; эта функция непрерывна и убывает, причем f (n) =

Так как , то данный ряд расходится.

1. Функциональные последовательности и ряды.

2. Сходимость функциональных рядов.

3. Сходимость степенных рядов.

4. Интервал и радиус сходимости степенного ряда.

1. Функциональные последовательности и ряды

Если каждому пÎN ставится в соответствие по определенному закону некоторая функция, определенная на одном и том же множестве ХÌR, то говорят, что на множестве Х определена функциональная последовательность 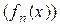. Отдельные функции

.

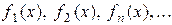называются членами этой последовательности, а множество Х - областью определения этой последовательности.

Взяв фиксированное , получим числовую последовательность 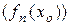. Если эта последовательность сходится, то точка х_о называется точкой сходимости функциональной последовательности 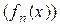. Множество всех точек сходимости функциональной последовательности её областью сходимости.

Пусть ЕÌХ - область сходимости функциональной последовательности 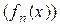, тогда для 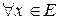существует предел

,

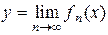причем этот предел у будет зависеть от выбора точки хÎЕ, т.е. 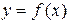, причем .

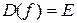Определение. Функция f(х) называется предельной функцией функциональной последовательности 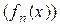на множестве Е, если для любой точки хÎЕ существует предел

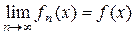. (1)

Определение. Пусть задана последовательность функций 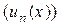, определенных на одном и том же множестве Х Ì R. Соединив члены этой последовательности знаком плюс, получим символ

, (1)

или сокращенно 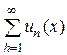, который называется функциональным рядом.

2. Определение 2. Функциональный ряд называется сходящимся в точке х_о, если сходится числовой ряд

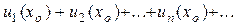. (2)

В этом случае точка х_о называется точкой сходимости функционального ряда (1). Множество всех точек сходимости функционального ряда называется областью сходимости этого ряда.

Пусть - п-ая частичная сумма функционального ряда (1), тогда если Е - область сходимости этого ряда, то для " х Î Е существует предел

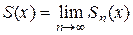, (3)

Решение. Члены этого ряда 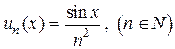определены на всей числовой прямой R. Для "х Î R имеем

.

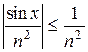Т.к. ряд - это ряд Дирихле с показателем a = 2, то этот ряд сходится, он является мажорантным рядом для ряда 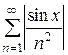на всей числовой прямой. По признаку сравнения положительных рядов данный ряд сходится абсолютно на R.

Пример 23. Найти область сходимости функционального ряда

.

Решение. Областью определения этого ряда является интервал (0;¥). Исследуем этот ряд на абсолютную сходимость, используя радикальный признак Коши абсолютной сходимости рядов. Общий член этого ряда . Имеем .

Ряд сходится абсолютно, если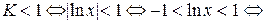

.

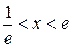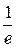Ряд сходится, если или ln x >1 Û x < или х > е. Таким образом, данный ряд расходится при 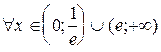. Осталось исследовать на сходимость данный ряд в точках 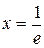и х = е, в которых предел K = 1.

При 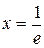имеем ln x = -1 данный ряд превращается в расходящийся ряд .

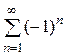При х = е следует, что ln x = 1 и снова из данного ряда получаем уже другой расходящийся ряд .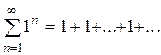

Таким образом, данный ряд сходится абсолютно на интервале

.

Пример 24. Исследовать на сходимость функциональный ряд

.

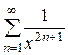Решение. Областью определения данного ряда является вся числовая прямая R, кроме единственной точки х = 0.

Исследуем этот ряд на абсолютную сходимость, применяя признак Даламбера абсолютной сходимости функциональных рядов. Общий член ряда , поэтому 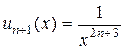. Найдем предел D:

.

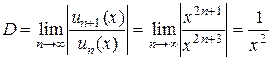Данный ряд сходится абсолютно, если условия D < 1, т.е.

;

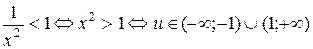этот ряд расходится, если .

Осталось исследовать на сходимость ряд в двух "подозрительных точках": х = ± 1. Как и в предыдущем примере доказывается, что в этих точках получаются расходящиеся ряды, соответственно

1+1+...+1+1...;

-1-1-...-1-1....

Таким образом, данный ряд сходится абсолютно на множестве
(-¥;-1) È (1;+ ¥), расходится на множестве [-1;0) È(0;1], а в точке х = 0 этот ряд не определен.

Пример 28. Найти область сходимости функционального ряда .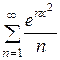

Решение. При " х Î R данный ряд - это положительный ряд, причем , т.е. члены ряда не меньше членов гармонического ряда. Так как гармонический ряд расходится, то данный ряд расходится всюду на числовой прямой, т.е. областью сходимости данного ряда является пустое множество.

Пример 29. Найти область сходимости функционального ряда .

Решение. Общий член данного ряда 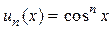. Применим к этому ряду радиальный признак Коши абсолютной сходимости рядов.

.

Отсюда следует, что данный ряд сходится абсолютно при " х Î R, где .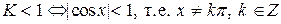

В точках 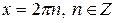этот ряд обращается в расходящийся числовой ряд 1+1+..+1+..., а в точках получается также расходящийся ряд -1+1-1+...+(-1)+....

Таким образом, данный ряд сходится абсолютно при всех значениях .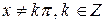

Замечание. Пусть Е - область сходимости функционального ряда, тогда для " х Î Е существует предел функционально последовательности (S_n (х)) частичных сумм этого ряда на множестве Е, причем сумма S (х) этого ряда является предельной функцией этой функциональной последовательности на множестве Е.

Отсюда следует, что характер сходимости функционального ряда (1) а множестве Е определяется характером сходимости функциональной последовательности (S_n (х)) частичных сумм этого ряда на множестве Е.

Поиск по сайту: