АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Смешанного произведения векторов

Читайте также:
  1. Алгебраические свойства векторного произведения
  2. Алгоритм вычисления произведения
  3. Белорусское искусство XVIII века. График Гершка Лейбович, резчик Ян Шмитт, художники Хеские. Слуцкие пояса и другие произведения декоративно-прикладного искусства данной эпохи.
  4. В хороших литературных произведениях особое значение придается реакциям.
  5. Векторного произведения
  6. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  7. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  8. Вопрос35. Предел Функции в точке и на бесконечности. Геометрическая иллюстрация определений. Предел постоянной. Предел суммы, частного, произведения. Предел элементарных функций.
  9. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
  10. Вычисление собственных значений и собственных векторов матриц.
  11. Глава девятая. Евангельский гуманизм в произведениях русских художников
  12. Для векторного произведения можно написать формулу, аналогичную (4).

Задача 1. Найти выражение для смешанного произведения векторов, заданных своими координатам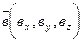и: , и .

Решение:

Пусть , тогда . С учетом свойств скалярного произведения векторов: .

Так как:

,

то следовательно, . Тогда .

Задача 2. Найти объем пирамиды, заданной координатами вершин: А1 (1;1;1), А2 (-2;1;-3), А3 (2;-3;0), А4 (0;-1;2).

Решение:

Образуем векторы . Найдем координаты векторов : 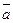(-3;0;-4), 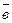(1;-4;-1), (-1;-2;1). Найдем смешанное произведение векторов :

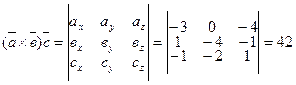
Поскольку объем параллелепипеда, построенного на векторах равен 42, то объем пирамиды А1А2А3А4 будет: .

Ответ: 7 (ед3).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)