АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнения прямой

Читайте также:
  1. VI Дифференциальные уравнения
  2. Алгебраические уравнения
  3. В отделение проктологии поступил больной с жалобами на кровотечение из стенок прямой кишки.
  4. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  5. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  6. Вопрос 43. Расчет времени начала снижения при заходе на посадку с прямой
  7. Врожденные заболевания прямой кишки
  8. Геометрическая оптика.отражение и преломление света. законы отражения и преломления.Зеркала и линзы.Уравнения для зеркал и линз.оптические приборы.
  9. Геометрический образ уравнения состояния.
  10. Дифференциальные уравнения 1 порядка с разделяющимися переменными
  11. Дифференциальные уравнения движения вязкой жидкости. Граничные условия.
  12. Дифференциальные уравнения и передаточные функции замкнутых систем управления

Уравнение F(х;у)= 0 называется уравнением линии l, если ему удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты каждой другой точки плоскости.

1) Ах+Ву+С= 0 - общее уравнение прямой. Коэффициенты А и В являются координатами вектора, перпендикулярного этой прямой. Угловой коэффициент этой прямой будет равен: 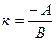. При С =0 прямая будет проходить через точку О (0;0), при А =0 прямая будет параллельна оси Ох, при А =0 и С =0 получим прямую, совпадающую с осью Ох. Аналогичны рассуждения при В =0 и В =0, С =0, относительно оси Оу.

2) у=кх+в - уравнение прямой с угловым коэффициентом. Эта прямая отсекает на оси ординат отрезок в и образует с положительным направлением оси Ох угол, тангенс которого равен к. При к >0, прямая будет проходить в направлении 1-го и 3-го координатных углов, а при к <0 - в направлении 2-го и 4-го координатных углов.

3) - уравнение прямой, проходящей через точки М1(х1;у1) и М2(х2;у2).

4) у-у0=к(х-х0) - уравнение пучка прямых, проходящих через точку М0(х0;у0).

5) 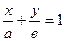- уравнение прямой "в отрезках", которые она отсекает на осях координат.

6) 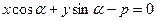- нормальное уравнение прямой.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)